Невырожденный треугольник

Значение понятия «Невырожденный треугольник»

Невырожденный треугольник — это треугольник, который имеет конечные стороны и углы, а также положительную площадь. Такой треугольник является основным объектом изучения геометрии и математики.

Значит, треугольник, который не является невырожденным, будет иметь одну или несколько из следующих характеристик:

• Одна или несколько сторон имеют нулевую длину. В этом случае треугольник превращается в отрезок или точку.
• Одна или несколько сторон имеют отрицательную длину. Это может происходить, когда точки, задающие стороны треугольника, расположены в неправильном порядке.
• Сумма длин двух сторон меньше третьей стороны. Такой треугольник называется вырожденным, и он не может существовать в двумерном пространстве.
• Один или несколько углов равны 0 или 180 градусов. Такие углы называются вырожденными углами и не отличаются от прямой линии или плоскости.

Имея эти определения в виду, мы можем утверждать, что для треугольника с конечными сторонами и положительной площадью справедливо понятие «невырожденный треугольник». Это базовое понятие является основой для изучения свойств и характеристик треугольников в геометрии.

Основные характеристики невырожденного треугольника

Что значит невырожденный треугольник? Невырожденный треугольник — это треугольник, у которого все три стороны положительной длины и никакие три точки, задающие его вершины, не лежат на одной прямой.

Вот основные характеристики, которые отличают невырожденный треугольник:

• Три стороны: невырожденный треугольник имеет три стороны, каждая из которых имеет положительную длину и является отрезком прямой между двумя вершинами.
• Три вершины: треугольник имеет три вершины, которые являются точками пространства или плоскости. Вершины образуют углы друг с другом.
• Три угла: треугольник состоит из трех углов, которые образуются между сторонами. Сумма всех углов в невырожденном треугольнике равна 180 градусам.
• Площадь: невырожденный треугольник имеет площадь, которая можно вычислить с использованием формулы Герона или других методов.
• Периметр: периметр невырожденного треугольника — это сумма всех его сторон. Он также может быть вычислен с помощью известных значений длин сторон.

Невырожденный треугольник является одной из основных фигур в геометрии. Он имеет множество свойств и характеристик, которые могут быть использованы для изучения его свойств и применения в различных математических и физических задачах.

Различия невырожденного треугольника от вырожденного

Треугольник — это геометрическая фигура, состоящая из трех отрезков, которые соединяются между собой в трех точках. Однако не все треугольники являются невырожденными, и это имеет свои особенности и значения.

Невырожденный треугольник (также известный как обычный треугольник) — это треугольник, у которого все три стороны имеют разную длину и все три угла не равны нулю и не равны 180 градусов. Невырожденный треугольник значит, что он имеет достаточно размеров и формы, чтобы считаться полноценным и функциональным треугольником.

Основное отличие невырожденного треугольника от вырожденного заключается в его свойствах и определениях. Невырожденный треугольник имеет три разные стороны и три угла, которые в сумме равны 180 градусов. Каждая сторона невырожденного треугольника соединяет две точки, и каждый угол образуется между двумя сторонами. Такой треугольник может быть измерен и описан с помощью геометрических формул и правил.

В то же время, вырожденный треугольник имеет особые свойства и определения. Он представляет собой треугольник, у которого все три стороны соединены в одной точке, а все три угла равны нулю или 180 градусов. Это значит, что его стороны и углы не образуют полноценной фигуры у треугольника и не могут быть измерены с помощью геометрических формул.

Таким образом, различия между невырожденным и вырожденным треугольниками заключаются в их свойствах и определениях. Невырожденный треугольник является полноценной геометрической фигурой с тремя разными сторонами и углами в сумме, равной 180 градусов, в то время как вырожденный треугольник не обладает такими свойствами и не может быть измерен с помощью геометрических формул.

Треугольник с двумя равными сторонами

Треугольник с двумя равными сторонами также называется равнобедренным треугольником. Он имеет две равные стороны, называемые боковыми сторонами, и одну сторону, называемую основанием.

Основание обычно выбирают горизонтально и обозначают буквой b, а боковые стороны — вертикально и обозначают буквами a. Угол между боковой стороной и основанием называется углом при основании, его обозначают буквой α.

Площадь равнобедренного треугольника можно вычислить по формуле: S = (b * a * sin α) / 2.

Кроме того, в равнобедренном треугольнике углы при вершине и при основании равны между собой, а сумма углов равна 180 градусам.

Примерами равнобедренных треугольников могут служить знак «Равенство» (=), знак «ПРАВО» на дорожных знаках, а также геометрические фигуры, которые имеют форму равнобедренного треугольника.

В другом месте

• Набор, содержащий одну точку, представляет собой вырожденный континуум.
• Объекты, такие как digon и monogon можно рассматривать как вырожденные случаи многоугольников : допустимы в общем абстрактном математическом смысле, но не являются частью исходной евклидовой концепции многоугольников.
• A случайная величина, которая может принимать только одно значение, имеет вырожденное распределение ; если это значение является действительным числом 0, то его плотность вероятности является дельта-функцией Дирака.
• Корни полинома называются вырожденными, если они совпадают, поскольку в общем случае n все корни многочлена n-й степени различны. Это использование переносится на собственные задачи: вырожденное собственное значение (то есть многократное совпадение корня характеристического многочлена ) — это такое, которое имеет более одного линейно независимого собственного вектора.
• В квантовая механика, любая такая кратность в собственных значениях оператора Гамильтона приводит к вырожденным уровням энергии. Обычно любое такое вырождение указывает на некоторую основную симметрию в системе.

Топ вопросов за вчера в категории образование

Образование 16.09.2023 23:41 2082 Ткачёв Витя.

Какое проверочное слово к слову ОГОРОД?

Ответов: 1

Образование 06.10.2023 16:43 831 Романов Ярослав.

Как правильно гулять» по лесу» или в» лесу»?

Ответов: 1

Образование 26.08.2023 14:06 2182 Пинчук Никита.

Какие фрукты начинаются на букву «Р»?

Ответов: 1

Образование 11.10.2023 21:09 1383 Ситникова Евгения.

Какое проверочное слово к слову ПРЕДПОЛАГАТЬ?

Ответов: 1

Образование 01.09.2023 05:01 2059 Зонова Виктория.

Какие фрукты начинаются на букву «Д»?

Ответов: 1

Образование 28.10.2023 10:34 1956 Угланова Яна.

Как решить: Для перевозки груза потребовалось 24 машины грузоподъём. 7,5 т?

Ответов: 1

Образование 10.10.2023 17:31 656 Швецов Степан.

Какое проверочное слово к слову иссЯкать?

Ответов: 1

Образование 04.10.2023 07:56 225 Самохвалов Ярослав.

Много очистков или очисток, как правильно?

Ответов: 1

Образование 07.11.2023 10:30 229 Ширяев Данил.

Какое проверочное слово к слову СОСТАВЛЯТЬ?

Ответов: 1

Образование 02.09.2023 05:24 1273 Салымгереев Акылбек.

Как правильно: по получении или по получению?

Ответов: 1

Сумма углов треугольника

В невырожденном треугольнике существуют разные типы углов:

1. Острые углы — углы, меньшие 90°;
2. Прямой угол — угол, равный 90°;
3. Тупой угол — угол, больший 90°, но меньший 180°.

Теорема о сумме углов треугольника утверждает, что в невырожденном треугольнике сумма углов всегда равна 180°. Это свойство можно доказать несколькими способами, например через параллельные линии или с использованием проекций.

Сумма углов в треугольнике можно найти с помощью формулы α + β + γ = 180°, где α, β и γ — углы треугольника.

Пользуясь этой формулой, можно определить тип треугольника по его углам:

• Треугольник с тремя острыми углами называется остроугольным, если все его углы меньше 90°;
• Треугольник с одним прямым углом называется прямоугольным;
• Треугольник с одним тупым углом называется тупоугольным.

Кроме того, сумма углов треугольника связана с его высотой. В прямоугольных треугольниках, высота проходит через прямой угол, а в остроугольных и тупоугольных треугольниках, высоты опускаются из вершин на стороны треугольника.

Также, сумма углов треугольника связана с площадью треугольника. С помощью высоты можно вычислить площадь треугольника по формуле S = 1/2 * a * h, где a — основание треугольника, h — высота. Или можно воспользоваться формулой S = 1/2 * b * c * sin(α), где b и c — боковые стороны треугольника, α — угол между ними.

В общем случае, треугольник можно классифицировать по различным свойствам, таким как равные стороны, равные углы, соотношение между сторонами внутри треугольника (например, теорема Пифагора), подобие с другими треугольниками и т.д.

Треугольник с двумя углами в 90 градусов

Такой треугольник называется «прямоугольным» и является основой для изучения тригонометрии. Два катета, пересекающиеся под прямым углом, обозначаются a и b, а гипотенуза — c. Известно, что гипотенуза всегда больше любого из катетов и можно вычислить ее длину по формуле:

c = √(a² + b²)

Прямоугольный треугольник встречается во многих областях, например, в геометрии, физике и инженерии. Он используется при расчете траектории движения тела, переноса картинок на экране компьютера и даже в космических экспедициях для ориентации в космосе.

• Примеры применения прямоугольного треугольника:
• Расчет длины кабеля, необходимого для соединения двух точек на разной высоте
• Расчет расстояния до недоступных объектов с помощью лазерного измерителя
• Расчет траектории падения парашютиста для безопасного приземления

Прямоугольный треугольник — важный элемент в повседневной жизни и науке. Его знание позволяет решать широкий круг задач, связанных с расчетами и конструированием. Основные теоремы, связанные с прямоугольным треугольником, были известны еще Древней Греции и с тех пор активно применяются в науке и технике.

Особенности невырожденного треугольника

Основная особенность невырожденного треугольника заключается в том, что его углы существуют и не равны нулю. Углы невырожденного треугольника могут быть остроугольными (меньше 90 градусов), тупоугольными (больше 90 градусов) или прямыми (равны 90 градусам).

Кроме того, невырожденный треугольник обладает следующими свойствами:

• Сумма всех трех углов треугольника всегда равна 180 градусов.
• Каждая сторона треугольника меньше суммы длин двух оставшихся сторон, что является неравенством треугольника.
• Высоты, проведенные из вершин треугольника на противоположные стороны, пересекаются в одной точке, называемой ортоцентром.
• Медианы треугольника, проведенные из вершин к серединам противоположных сторон, пересекаются в одной точке, называемой центроидом.
• Биссектрисы треугольника, проведенные из вершин к противоположным углам, пересекаются в одной точке, называемой центральным угловым центром.
• Отец всех треугольников — треугольник, являющийся каждой из своих сторон.

Эти особенности делают невырожденный треугольник одной из основных геометрических фигур, используемых в различных областях науки и техники.

Практическое применение невырожденных треугольников

Невырожденный треугольник — это треугольник, у которого все стороны имеют ненулевую длину и все углы не равны нулю. Такой треугольник является основой геометрии и находит широкое применение в различных практических задачах.

1. Инженерия:

В инженерии невырожденные треугольники используются для измерения и оценки расстояний, высот, углов и площадей. Инженеры часто используют теорему Пифагора и тригонометрию для решения проблем и построения структур. Невырожденные треугольники также используются в машиностроении и строительстве для расчета нагрузок, сил и устойчивости конструкций.

2. Картография:

В картографии невырожденные треугольники используются для построения карт и определения координатных систем. С помощью треугольников можно измерить расстояние между точками на карте и определить их географические координаты.

3. Геодезия:

В геодезии невырожденные треугольники используются для измерения и определения формы и размеров Земли. Геодезисты строят сети геодезических треугольников, измеряя их стороны и углы. Эти данные помогают определить геодезическую длину и форму поверхности Земли, а также международные геодезические сети.

4. Кристаллография:

В кристаллографии невырожденные треугольники используются для определения структуры кристаллов. Кристаллы имеют регулярные и повторяющиеся структуры, которые часто выражаются в виде невырожденных треугольников. Изучение кристаллов и их структуры помогает ученым понять и предсказать их свойства и потенциальное применение в различных областях, включая материаловедение, химию и физику.

Суммируя, невырожденные треугольники играют важную роль в различных областях и являются основой для решения множества практических задач. Их свойства и теоремы позволяют инженерам, геодезистам, картографам и ученым более точно измерять и описывать физические и географические объекты, а также прогнозировать и предсказывать их характеристики и поведение.

Инженерное строительство

Инженерное строительство – это область, занимающаяся проектированием, разработкой и строительством различных инженерных сооружений, которые включают в себя дороги, мосты, тоннели и другие сложные инженерные объекты.

Одним из важных элементов инженерного строительства являются треугольники. Треугольник – это геометрическая фигура, которая образуется из трех прямых отрезков, соединяющих три точки. Он имеет три стороны и три угла.

Невырожденный треугольник – это специальный тип треугольника, у которого все его стороны и углы не равны нулю. Такой треугольник считается непосредственным и имеет реальное существование в пространстве.

Значение невырожденного треугольника в инженерном строительстве заключается в его многогранной прочности и устойчивости. Треугольник является самой прочной фигурой среди всех возможных многоугольников. Его структура делает его идеальным для использования в строительстве мостов, каркасов зданий и других конструкций, где необходима высокая нагрузочная способность.

Инженерное строительство активно использует принципы геометрии и геометрические фигуры, такие как треугольники, для создания устойчивых и надежных конструкций. Использование невырожденных треугольников позволяет строить прочные и долговечные сооружения, способные выдерживать большие нагрузки и внешние воздействия.

Основные формулы

Для каждого треугольника существует набор формул, с помощью которых можно определить его элементы. Чаще всего приходится выяснять длины сторон, площадь, высоты и периметр. При этом если известны боковые грани, можно найти практически любые остальные параметры.

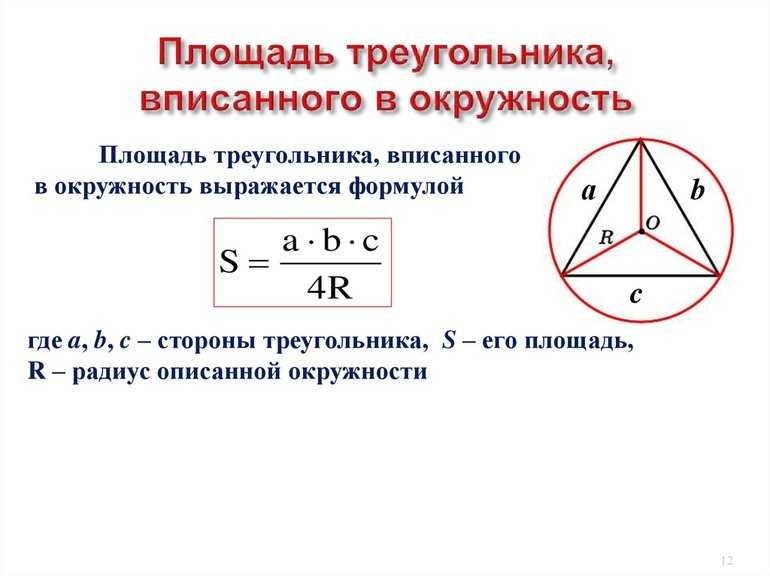
Вокруг правильной фигуры можно описать круг, причём окружность можно и вписать в середину. Что интересно, их центры совпадут между собой и с местом пересечения высот. В этом случае радиус внешнего круга равняется R = (a * √‎3) / 3 = a / 2 * sin (a), а внутреннего: r = (a * √‎3) / 6 = R / 2. Чтобы найти высоту, зная радиус, используют выражение: h = (3 *R) / 2. Кроме этой формулы, довольно часто применяют равенство, связывающее сторону и перпендикуляр: h = (a * √‎3) / 2.

Доказательство верности формулы для нахождения радиуса вписанной окружности можно построить исходя из выражения, справедливого к равнобедренной фигуре: r = b / 2 √(‎(2 a — b) / (2 a + b)). Так как стороны равны, то a = b. Получается, что r = a / 2 √‎(2a — a) / (2a + a) = (a / 2) * √‎(1 / 3) = a / (2 * √‎3) = (a √‎3) / 6.

Чтобы определить длину стороны, нужно знать высоту и теорему Пифагора. Согласно ей, квадрат гипотенузы находится как сумма квадратов высоты и длины разделённого основания. Применяя теорему к правильной фигуре, можно записать: AB2 = h2 + (AB / 2)2. Это равенство решают следующим образом: AB2 = h2 + AB2 / 22. Выражение можно преобразовать в вид: (3a2 / 4) = h 2 → a 2 = (4 * h2) / 3 → a 2 = √‎((4 * h2) / 3) → a = (2 * h) / √3.

Из других существующих формул можно перечислить те, что чаще всего применяют при решении примеров:

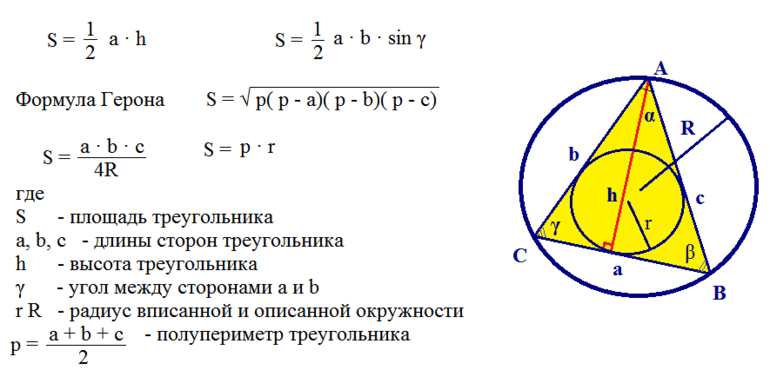
1. Площадь. Находят из выражения: S = (a 2 * √3) / 4. Вывести эту формулу довольно просто. Если взять за основу, что равенство для площади верно, то исходя из свойств фигуры можно записать: S = ½ * a2 * sin 60 = ½ * a2 * √3 / 2 = (√3 / 4) * a2. Что и следовало доказать.
2. Периметр. Чтобы его определить, нужно сложить длины всех сторон, но так как в правильной фигуре они равны, можно воспользоваться формулой: P = 3 * a.

Существуют ещё 2 значимые теоремы: косинусов и синусов. Согласно первой, квадрат стороны фигуры будет ранятся удвоенному произведению двух оставшихся отрезков и косинусу угла между ними, отнятому из суммы квадратов: a2 = b2 + c2 — 2 * b * c * cos (a). Согласно же второй, длины отрезков пропорциональны синусам углов, лежащих напротив: a / sin (a) = b / sin (b) = c / sinс.

В геометрии

Коническое сечение

Вырожденная коника — это коническое сечение (плоская кривая второй степени , определяемая полиномиальным уравнением второй степени), которая не может быть неприводимой кривой.

• A точкой, является вырожденная окружность, а именно, радиус 0.
• Линия — это вырожденный случай параболы, если парабола находится на касательная плоскость. В инверсной геометрии линия является вырожденным случаем окружности с бесконечным радиусом.
• Две параллельные линии также образуют вырожденную параболу.
• A отрезок можно рассматривать как вырожденный случай эллипса, в котором малая полуось переходит в ноль, а фокусы переходят в конечных точек, а эксцентриситет переходит в единицу.
• Окружность можно представить как вырожденный эллипс, поскольку эксцентриситет приближается к нулю.
• Эллипс также может вырождаться в одну точку.
• A гипербола может вырождаться в две линии, пересекающиеся в точке, через семейство гипербол, имеющих эти линии как общие асимптоты.

Треугольник

A вырожденный треугольник имеет коллинеарные вершины и нулевую площадь и, таким образом, совпадает с отрезком, покрытым дважды (если три вершины не равны; в противном случае треугольник вырождается в одну точку). Если три вершины попарно различны, он имеет два угла 0 ° и один угол 180 °. Если две вершины равны, у него один угол 0 ° и два неопределенных угла.

Прямоугольник

• Отрезок линии — это вырожденный случай прямоугольника , длина стороны которого равна 0.
• Для любого непустого подмножества S ⊆ {1, 2,…, n} {\ displaystyle S \ substeq \ {1,2, \ ldots, n \}}, существует ограниченный выровненный по оси вырожденный прямоугольник

  R ≜ {x ∈ R n: xi = ci (для i ∈ S) и ai ≤ xi ≤ bi (для i ∉ S)} {\ displaystyle R \ Triangleq \ left \ {\ mathbf {x} \ in \ mathbb {R} ^ {n}: x_ {i} = c_ {i} \ ({\ text {for}} i \ in S) {\ text {и}} a_ {i} \ leq x_ {i} \ leq b_ {i} \ ({\ text {for}} i \ notin S) \ right \}}

  где x ≜ {\ displaystyle \ mathbf {x} \ треугольник q \ left }и ai, bi, ci {\ displaystyle a_ {i}, b_ {i}, c_ {i}}являются постоянными (с ai ≤ bi {\ displaystyle a_ {i} \ leq b_ {i }}для всех i {\ displaystyle i}). Количество вырожденных сторон R {\ displaystyle R}- это количество элементов подмножества S {\ displaystyle S}. Таким образом, может быть всего одна вырожденная «сторона» или целых n {\ displaystyle n}(в этом случае R {\ displaystyle R}сводится к одноэлементной точке).

Выпуклый многоугольник

A выпуклый многоугольник является вырожденным, если хотя бы две последовательные стороны совпадают хотя бы частично, или хотя бы одна сторона имеет нулевую длину, или хотя бы один угол равен 180 °. Таким образом, вырожденный выпуклый многоугольник с n сторонами выглядит как многоугольник с меньшим числом сторон. В случае треугольников это определение совпадает с тем, что было дано выше.

Выпуклый многогранник

A выпуклый многогранник вырожден, если либо две смежные грани копланарны, либо два ребра являются выровнен. В случае тетраэдра это эквивалентно тому, что все его вершины лежат в одной плоскости, что дает ему объем нуля.

Стандартный тор

В контекстах, где разрешено самопересечение, сфера представляет собой вырожденный стандартный тор, ось вращения которого проходит через центр образующий круг, а не за его пределами.

Значимость невырожденных треугольников

Невырожденные треугольники являются основным строительным блоком геометрии и имеют большое значение в различных научных и практических областях. Они широко используются в архитектуре, инженерии, физике, графике и других науках.

Вот несколько основных причин, почему невырожденные треугольники являются важными:

1. Определение формы и размера: Невырожденные треугольники обладают четко определенной формой и размером. Используя их в качестве основного элемента для построения, архитекторы и инженеры могут создавать прочные и устойчивые сооружения. Например, пирамиды в Египте и готические соборы в Европе строятся на основе треугольников.
2. Вычисления и измерения: Треугольники являются одной из наиболее изученных геометрических фигур. Их свойства и формулы используются для вычислений и измерений в различных областях. Например, в геодезии треугольники используются для определения расстояний и углов на земной поверхности.
3. Графическое моделирование и анимация: Треугольники используются как основные элементы в компьютерной графике и анимации. В трехмерной графике объекты обычно представляются в виде множества треугольников, которые затем обрабатываются компьютером для создания реалистичных изображений и анимации.
4. Триангуляция: Треугольники играют важную роль в геометрии и алгоритмах триангуляции. Триангуляция представляет собой разбиение геометрической фигуры на невырожденные треугольники. Этот процесс используется в различных областях, таких как картография, сеточное моделирование и компьютерная графика.
5. Перспектива и пропорции: Треугольники используются для создания эффекта перспективы и определения пропорций в изображении. В искусстве и дизайне треугольники могут использоваться для создания глубины и тримерного вида, а также для соблюдения пропорций и гармонии в композиции.

Таким образом, невырожденные треугольники играют важную роль в различных областях, от строительства и наук о материалах до компьютерной графики и искусства. Понимание и использование треугольников позволяют нам лучше понять и описать мир вокруг нас.

Где применяют Вырожденный треугольник?

Вырожденный треугольник – это треугольник, у которого длина одной из его сторон равна сумме длин двух других, что делает его плоскость вырожденной в точку. Этот тип треугольников используется в различных областях, включая математику, физику, астрономию и технические науки.

В математике, вырожденные треугольники обнаруживаются в различных геометрических задачах. Например, они могут быть использованы для указания касательной к окружности в геометрии, для доказательства теорем Пифагора и для определения углов между двумя плоскостями.

В физике и астрономии, вырожденные треугольники используются в моделировании процессов деформации материалов и для определения расстояний в космических миссиях. Они также используются для моделирования дополнительных измерений в квантовой механике и гравитации.

В технических науках, вырожденные треугольники используются для проектирования и конструирования конструкций, включая сооружения мостов и зданий высокой точности. Они также используются в компьютерной графике для создания более сложных объектов, таких как корпуса самолетов и автомобилей.

Практическое применение вырожденных треугольников

Вырожденные треугольники, несмотря на свою необычную структуру, имеют некоторые практические применения. Ниже приведены некоторые из них:

Графика и компьютерное моделирование: В компьютерной графике вырожденные треугольники могут быть использованы для представления точек или линий, что позволяет более эффективно использовать компьютерные ресурсы.

Аппроксимация и интерполяция: Вырожденные треугольники могут быть использованы для аппроксимации или интерполяции данных, особенно в случае, когда имеется недостаточно информации для построения обычного треугольника.

Треугольные сетки: В компьютерной графике и вычислительной геометрии треугольные сетки широко используются для описания поверхности объектов и их моделирования. Вырожденные треугольники могут быть включены в такие сетки для более эффективного представления данных.

Анализ и оптимизация: Вырожденные треугольники также могут быть использованы для анализа и оптимизации различных процессов, например, при расчете максимальной или минимальной площади треугольника с заданными ограничениями.

Хотя вырожденные треугольники не являются типичными и не встречаются так часто, как обычные треугольники, они все же имеют свои применения и могут быть полезны в определенных ситуациях.

[править] Свойства и особенности треугольников

Трём точкам пространства, не лежащим на одной прямой (и образуемому ими невырожденному треугольнику), обязательно соответствует одна и только одна плоскость. Это весьма уникально — так как меньшему количеству точек соответствуют прямая и точка, а уже четыре точки могут находится вне единой плоскости.

Треугольник — это часть плоскости, ограниченная минимально возможным количеством сторон. Любой многоугольник можно точно разбить на треугольники, лишь связав его вершины отрезками, не пересекающими его стороны. С некоторым приближением, на треугольники можно разбить поверхность любой формы, как на плоскости так и в пространстве. Процесс разбиения на треугольники называется триангуляция.

Существует раздел математики, целиком посвящённый изучению закономерностей треугольников — Тригонометрия.

Треугольник, когда не вырожден — всегда выпуклый многоугольник.

Для треугольника всегда существует одна вписанная и одна описанная окружность.

Нормированное векторное пространство

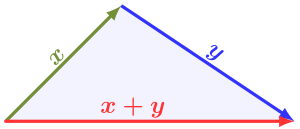Неравенство треугольника для норм векторов.

В нормированное векторное пространство V, одно из определяющих свойств норма это неравенство треугольника:

‖Икс+у‖≤‖Икс‖+‖у‖∀Икс,у∈V{ displaystyle displaystyle | x + y | leq | x | + | y | quad forall , x, y in V}

то есть норма не больше суммы норм двух векторов. Это также называется субаддитивность. Чтобы любая предлагаемая функция вела себя как норма, она должна удовлетворять этому требованию.

Если нормированное пространство евклидов, или, в более общем смысле, строго выпуклый, тогда ‖Икс+у‖=‖Икс‖+‖у‖{ Displaystyle | х + у | = | х | + | у |} если и только если треугольник, образованный Икс, у, и Икс + у, является вырожденным, то естьИкс и у находятся на одном луче, т.е. Икс = 0 или у = 0, илиИкс = α y для некоторых α > 0. Это свойство характеризует строго выпуклые нормированные пространства, такие как ℓ_п пространства с 1 < п < ∞. Однако есть нормированные пространства, в которых это неверно. Например, рассмотрим самолет с ℓ₁ норма ( Манхэттенское расстояние ) и обозначить Икс = (1, 0) и у = (0, 1). Тогда треугольник, образованныйИкс, у, и Икс + у, невырожден, но

‖Икс+у‖=‖(1,1)‖=|1|+|1|=2=‖Икс‖+‖у‖.{ Displaystyle | х + у | = | (1,1) | = | 1 | + | 1 | = 2 = | х | + | у |.}

Примеры норм

Абсолютное значение как норма для реальная линия. Чтобы быть нормой, неравенство треугольника требует, чтобы абсолютная величина удовлетворять для любых реальных чисел Икс и у:

|Икс+у|≤|Икс|+|у|,{ Displaystyle | х + у | Leq | х | + | у |,}

что он делает.

Доказательство:

−|Икс|≤Икс≤|Икс|{ displaystyle — left vert x right vert leq x leq left vert x right vert}

−|у|≤у≤|у|{ displaystyle — left vert y right vert leq y leq left vert y right vert}

После добавления

−(|Икс|+|у|)≤Икс+у≤|Икс|+|у|{ Displaystyle — ( влево верт х вправо верт + влево верт у вправо верт) Leq х + у Leq влево верт х вправо верт + влево верт у вправо vert}

Используйте тот факт, что |б|≤а⇔−а≤б≤а{ displaystyle left vert b right vert leq a Leftrightarrow -a leq b leq a}(с участием б заменяется Икс+у и а от |Икс|+|у|{ displaystyle left vert x right vert + left vert y right vert}), у нас есть

|Икс+у|≤|Икс|+|у|{ Displaystyle | х + у | Leq | х | + | у |}

Неравенство треугольника полезно в математический анализ для определения наилучшей верхней оценки размера суммы двух чисел в терминах размеров отдельных чисел.

Существует также более низкая оценка, которую можно найти с помощью обратное неравенство треугольника в котором говорится, что для любых действительных чисел Икс и у:

|Икс−у|≥||Икс|−|у||.{ displaystyle | x-y | geq { bigg |} | x | — | y | { bigg |}.}

Внутренний продукт как норма в внутреннее пространство продукта. Если норма возникает из внутреннего произведения (как в случае евклидовых пространств), то неравенство треугольника следует из Неравенство Коши – Шварца следующим образом: данные векторы Икс{ displaystyle x} и у{ displaystyle y}, и обозначив внутренний продукт как ⟨Икс,у⟩{ Displaystyle langle х, у rangle}:

‖Икс+у‖2{ Displaystyle | х + у | ^ {2}}	=⟨Икс+у,Икс+у⟩{ displaystyle = langle x + y, x + y rangle}
	=‖Икс‖2+⟨Икс,у⟩+⟨у,Икс⟩+‖у‖2{ displaystyle = | x | ^ {2} + langle x, y rangle + langle y, x rangle + | y | ^ {2}}
	≤‖Икс‖2+2|⟨Икс,у⟩|+‖у‖2{ Displaystyle Leq | х | ^ {2} +2 | langle x, y rangle | + | y | ^ {2}}
	≤‖Икс‖2+2‖Икс‖‖у‖+‖у‖2{ Displaystyle Leq | х | ^ {2} +2 | х | | у | + | у | ^ {2}} (по неравенству Коши – Шварца)
	=(‖Икс‖+‖у‖)2{ Displaystyle = влево ( | х | + | у | вправо) ^ {2}}.

Неравенство Коши – Шварца превращается в равенство тогда и только тогда, когда Икс и улинейно зависимы. Неравенство⟨Икс,у⟩+⟨у,Икс⟩≤2|⟨Икс,у⟩|{ displaystyle langle x, y rangle + langle y, x rangle leq 2 | langle x, y rangle |}превращается в равенство для линейно зависимых Икс{ displaystyle x} и у{ displaystyle y}тогда и только тогда, когда один из векторов Икс или у это неотрицательный скаляр другого.

Извлечение квадратного корня из окончательного результата дает неравенство треугольника.

п-норма: обычно используемой нормой является п-норма:

‖Икс‖п=(∑я=1п|Икся|п)1п ,{ Displaystyle | х | _ {p} = left ( sum _ {i = 1} ^ {n} | x_ {i} | ^ {p} right) ^ {1 / p} ,}

где Икс_я компоненты вектора Икс. Для п = 2 то п-норма становится Евклидова норма:

‖Икс‖2=(∑я=1п|Икся|2)12=(∑я=1пИкся2)12 ,{ Displaystyle | х | _ {2} = влево ( сумма _ {я = 1} ^ {п} | х_ {я} | ^ {2} вправо) ^ {1/2} = влево ( sum _ {i = 1} ^ {n} x_ {i} ^ {2} right) ^ {1/2} ,}

который Теорема Пифагора в п-размеры, очень частный случай, соответствующий внутренней норме продукта. Кроме случая п = 2, то п-норма не внутренняя норма продукта, потому что она не удовлетворяет закон параллелограмма. Неравенство треугольника для общих значений п называется Неравенство Минковского. Он принимает вид:

‖Икс+у‖п≤‖Икс‖п+‖у‖п .{ displaystyle | x + y | _ {p} leq | x | _ {p} + | y | _ {p} .}