Правильный пятиугольник — построение, свойства и формулы

Содержание

• 1 Правильные пятиугольники
  • 1.1 Вывод формулы площади
  • 1.2 Inradius
  • 1.3 Хорды ​​от описанной окружности к вершины
  • 1.4 Точка на плоскости
  • 1.5 Построение правильного пятиугольника
    • 1.5.1 Метод Ричмонда
    • 1.5.2 Круги Карлайла
    • 1.5.3 Использование t ригонометрия и теорема Пифагора
    • 1.5.4 † Доказательство того, что cos 36 ° = 1 + 5 4 {\ displaystyle {\ tfrac {1 + {\ sqrt {5}}} {4}}}
    • 1.5.5 Задана длина стороны
  • 1.6 Метод Евклида
  • 1.7 Физические методы
  • 1.8 Симметрия
• 2 Равносторонние пятиугольники
• 3 Циклические пятиугольники
• 4 Общие выпуклые пятиугольники
• 5 Графики
• 6 Примеры пятиугольников
  • 6.1 Растения
  • 6.2 Животные
  • 6.3 Минералы
  • 6.4 Искусственные
• 7 Пентагонов в мозаике
• 8 Пентагонов в многогранниках
• 9 См. Также
• 10 Встроенные примечания и ссылки
• 11 Внешние ссылки

Основные понятия введения в стереометрию

Стереометрия — это раздел геометрии, в котором изучаются свойства фигур в пространстве.Слово «стереометрия» происходит от греческих слов «στερεοσ» — объемный, пространственный и «μετρεο» — измерять.

Многогранник представляет собой геометрическое тело, ограниченное конечным числом плоских многоугольников, любые два из которых, имеющие общую сторону, не лежат в одной плоскости. При этом сами многоугольники называются гранями, их стороны – ребрами многогранника, а их вершины – вершинами многогранника.

Фигура, образованная всеми гранями многогранника, называется его поверхностью (полной поверхностью), а сумма площадей всех его граней – площадью (полной) поверхности.

Куб – это многогранник, имеющий шесть граней, которые являются равными квадратами. Стороны квадратов называются ребрами куба, а вершины – вершинами куба.

Параллелепипед – это многогранник, у которого шесть граней и каждая из них – параллелограмм. Стороны параллелограммов называются ребрами параллелепипеда, а их вершины – вершинами параллелепипеда. Две грани параллелепипеда называются противолежащими, если они не имеют общего ребра, а имеющие общее ребро называются смежными. Иногда какие-нибудь две противолежащие грани параллелепипеда выделяются и называются основаниями, тогда остальные грани – боковыми гранями, а их стороны, соединяющие вершины оснований параллелепипеда, – его боковыми ребрами.

Прямой параллелепипед – это такой параллелепипед, у которого боковые грани – прямоугольники.

Прямоугольный параллелепипед – это параллелепипед, у которого все грани – прямоугольники. Заметим, что всякий прямоугольный параллелепипед является прямым параллелепипедом, но не любой прямой параллелепипед есть прямоугольный.

Две вершины параллелепипеда, не принадлежащие одной грани, называются противолежащими. Отрезок, соединяющий противолежащие вершины параллелепипеда, называется диагональю параллелепипеда. У параллелепипеда всего четыре диагонали.

Призма (n-угольная) – это многогранник, у которого две грани – равные n-угольники, а остальные n граней – параллелограммы. Равные n-угольники называются основаниями, а параллелограммы – боковыми гранями призмы.

Прямая призма – это такая призма, у которой боковые грани – прямоугольники. Правильная n-угольная призма – это призма, у которой все боковые грани – прямоугольники, а ее основания – правильные n-угольники.

Сумма площадей боковых граней призмы называется площадью ее боковой поверхности (обозначается Sбок). Сумма площадей всех граней призмы называется площадью поверхности призмы (обозначается Sполн).

Пирамида (n-угольная) – это многогранник, у которого одна грань – какой-нибудь n-угольник, а остальные n граней – треугольники с общей вершиной; n-угольник называется основанием; треугольники, имеющие общую вершину, называются боковыми гранями, а их общая вершина называется вершиной пирамиды. Стороны граней пирамиды называются ее ребрами, а ребра, сходящиеся в вершине, называются боковыми.

Сумма площадей боковых граней пирамиды называется площадью боковой поверхности пирамиды (обозначается Sбок). Сумма площадей всех граней пирамиды называется площадью поверхности пирамиды (площадь поверхности обозначается Sполн).

Правильная n-угольная пирамида – это такая пирамида, основание которой – правильный n-угольник, а все боковые ребра равны между собой. У правильной пирамиды боковые грани – равные друг другу равнобедренные треугольники.

Треугольная пирамида называется тетраэдром, если все ее грани – равные правильные треугольники. Тетраэдр является частным случаем правильной треугольной пирамиды (т.е. не каждая правильная треугольная пирамида будет тетраэдром).

Свойства правильного пятиугольника

Правильный пятиугольник — это пятиугольник, у которого все стороны равны друг другу и все углы равны 108 градусам.

1. Равные стороны: Все пять сторон правильного пятиугольника равны друг другу. Это означает, что длина каждой стороны пятиугольника одинакова.
2. Равные углы: Все углы правильного пятиугольника равны между собой и составляют 108 градусов. Каждый угол пятиугольника равен 108 градусам.
3. Сумма углов: Сумма всех углов правильного пятиугольника равна 540 градусам. Это можно вычислить, умножив 108 на 5.
4. Центральная симметрия: Правильный пятиугольник обладает центральной симметрией, что означает, что его можно вращать вокруг центра на некоторый угол и при этом он будет выглядеть абсолютно одинаково.
5. Площадь: Площадь правильного пятиугольника можно вычислить с помощью специальных формул, которые зависят от длины стороны пятиугольника.

Правильные пятиугольники встречаются в различных областях науки и искусства. Некоторые примеры правильных пятиугольников включают звезду с пятью вершинами и монету в некоторых странах.

Определение

Вершина угла

Вершина угла — это точка, окуда берут начало два луча.

Вершина угла — это точка, откуда берут начало два луча; где сходятся два отрезка; где две прямые пересекаются; где любая комбинация лучей, отрезков и прямых, образующих две (прямолинейные) «стороны», которые сходятся в одной точке.

Вершина многоугольника многогранника

Вершина — это угловая точка многоугольника или многогранника (любой размерности), иначе говоря его 0-мерная граней.

В многоугольнике вершина называется «выпуклой», если внутренний угол многоугольника меньше π радиан (180° — два прямых угла). В противном случае вершина называется «вогнутой».

Более обще, вершина многогранника является выпуклой, если пересечение многогранника с достаточно малой сферой, имеющей вершину в качестве центра, представляет собой выпуклую фигуру; в противном же случае вершина является вогнутой.

Вершины многогранника связаны с вершинами графа, поскольку многогранника является графом, вершины которого соответствуют вершинам многогранника, а следовательно, граф многогранника можно рассматривать как одномерный симплициальный комплекс, вершинами которого служат вершины графа. Однако, в теории графов вершины могут иметь менее двух инцидентных рёбер, что обычно не разрешается для вершин геометрических. Также имеется связь между геометрическими вершинами и вершинами кривой, точками экстремумов её кривизны — вершины многоугольника в некотором смысле являются точками бесконечной кривизны, и, если многоугольник приблизить гладкой кривой, точки экстремальной кривизны будут лежать вблизи вершин многоугольника. Однако, приближение многоугольника с помощью гладкой кривой даёт дополнительные вершины в точках минимальной кривизны.

Вершины плоских мозаик

Вершина плоской мозаики (замощения) — это точка, где встречаются три и более плиток мозаики, но не только: плитки замощения также являются многоугольниками, а вершины мозаики являются вершинами этих плиток. Более обще, замощение можно рассматривать как вид топологического CW-комплекса. Вершины других видов комплексов, таких как симплициальные, — это грани нулевой размерности.

Определение пятиугольника

Пятиугольник — это геометрическая фигура, которая состоит из пяти вершин и пяти сторон. Все стороны пятиугольника равны между собой, а углы при вершинах составляют 108 градусов.

Пятиугольник является одним из видов многоугольников, которые имеют более двух вершин и сторон. Он также называется пятиугольным полигоном.

У пятиугольника общая длина его сторон суммируется, чтобы получить его периметр. Периметр пятиугольника можно найти, сложив длины всех его сторон. Чтобы найти площадь пятиугольника, необходимо знать длину его сторон и использовать соответствующую формулу.

Расположение вершин пятиугольника может быть разным. На рисунке ниже показан пример пятиугольника с указанием вершин и сторон:

Пятиугольники можно классифицировать в зависимости от различных параметров, например, в выпуклые или невыпуклые, правильные или неправильные. Правильный пятиугольник — это пятиугольник, у которого все стороны и углы равны. Неправильный пятиугольник — это пятиугольник, у которого стороны и/или углы не равны.

Примеры неправильных пятиугольников:

• Пятиугольник с разными длинами сторон;
• Пятиугольник с углами, не равными 108 градусам;
• Пятиугольник с пересекающимися сторонами.

Примеры правильных пятиугольников:

• Пентагон;
• Звезда с пятью равными сторонами;
• Построенный с использованием геометрического инструмента «компас».

Изучение свойств и характеристик пятиугольников является важной задачей в геометрии и имеет широкое применение в различных областях, таких как архитектура, дизайн, инженерия и т. д

Определение геометрической фигуры

Геометрическая фигура — это совокупность определенных элементов, таких как стороны, углы, вершины, которые образуют определенную форму в двухмерном или трехмерном пространстве.

В геометрии существует множество различных фигур, каждая из которых имеет свои особенности и характеристики. Одной из таких фигур является пятиугольник.

Пятиугольник — это геометрическая фигура, состоящая из пяти отрезков, соединенных последовательно в плоскости друг с другом. У пятиугольника есть пять сторон, пять вершин и пять углов.

Название «пятиугольник» уже указывает на то, сколько у него вершин — пять. Вершины пятиугольника образуются там, где соединяются две стороны.

Форма пятиугольника

Пятиугольник — это многоугольник, который состоит из пяти вершин и пяти сторон.

Чтобы определить, сколько вершин у пятиугольника, достаточно просмотреть его форму. В данном случае, пятиугольник имеет пять вершин.

Форма	Количество вершин
Треугольник	3
Четырехугольник	4
Пятиугольник	5

Таким образом, пятиугольник имеет пять вершин.

Сумма углов выпуклого многоугольника

Научимся находить сумму углов выпуклого четырёхугольника, не только внешних, но и внутренних. Но сначала определим, какие углы называются внутренними углами выпуклого многоугольника.

Внутренним называется угол между смежными сторонами.

Например, ∠ABC является внутренним для ABCDEF.

Внешним называют угол между стороной фигуры и линейным продолжением близлежащего отрезка.

Например, ∠LBC является внешним углом для ABCDEF.

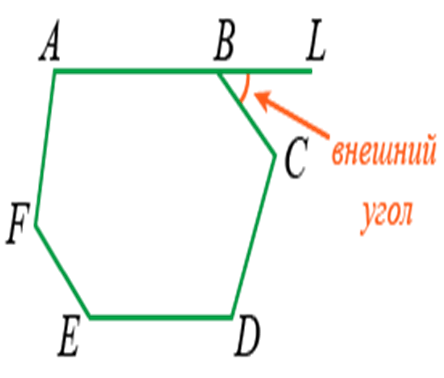
Правило: сумма углов выпуклого многоугольника всегда равно числу его сторон. Это определение относится ко всем углам.

Это значит, чтобы найти количество углов, достаточно посчитать количество всех его сторон. Значит сумма углов четырехугольника будет равна четырем.

Сумма внутренних углов

Правило для нахождения суммы углов гласит: чтобы найти сумму всех внутренних углов выпуклого многоугольника, нужно умножить уменьшенное на 2 количество его сторон на 180°.

Обозначения выглядят следующим образом:

• сумма углов – s;
• число сторон – n;
•  два прямых угла (2 · 90 = 180°) – 2d.

Формула многоугольника для нахождения суммы углов: s = 2d · (n – 2).

Найти сумму углов также можно с помощью деления фигуры на треугольники. Она будет равна сумме углов всех треугольников (180° · n).

Пример:

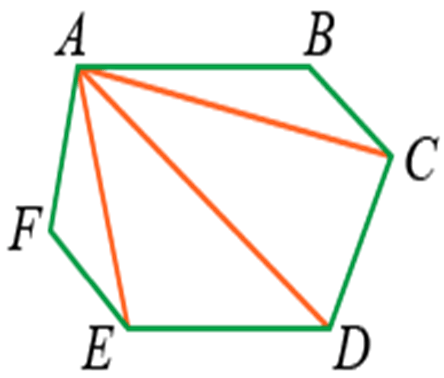
Если у фигуры 4 треугольника, то сумму всех углов находим по следующей формуле: s = 2d (n — 2) = 180 · 4 = 720°.

Это означает, что сумма внутренних углов – это постоянная величина, которая зависит от количества его сторон.

Нет времени решать самому?

Наши эксперты помогут!

Контрольная

| от 300 ₽ |

Реферат

| от 500 ₽ |

Курсовая

| от 1 000 ₽ |

Нужна помощь

Использование пятиугольника в викканских и языческих традициях

Пятиугольник, также известная как пентаграмма, является символом, который использовался во многих культурах на протяжении всей истории, в том числе в викканских и языческих традициях. Пятиугольник состоит из пяти точек, расположенных в форме звезды, каждая из которых представляет один из пяти элементов: воздух, воду, огонь, землю и дух. Этот символ часто рассматривается как представление баланса и гармонии между этими элементами.

Число 4: В викканских и языческих традициях число четыре часто ассоциируется с четыре направления: север, юг, восток и запад. Говорят, что эти направления соответствуют физическим элементам: земле, огню, воздуху и воде. Пятиугольник с его пятью вершинами представляет собой добавление духа к этим четырем элементам, создавая более полную и сбалансированную систему.

Еще одна интерпретация числа четыре и пятиугольника заключается в том, что они представляют четыре сезона и цикл жизни и смерти. Четыре сезона, соответствующие солнцестояниям и равноденствиям, рассматриваются как напоминание о постоянном цикле рождения, роста, распада и обновления в природе. Пятая точка пятиугольника представляет собой вечный цикл жизни и смерти, неизменную сущность, которая лежит в основе всего сущего.

Пятиугольник также связан с концепцией защиты. В викканских и языческих традициях пятиугольник часто рассматривается как символ защиты от негативных энергий и сил. Говорят, что пять вершин звезды представляют пять элементов, которые можно призвать для создания защитного щита вокруг человека или объекта с пятиугольником.

Элемент	Соответствующее направление	Связанные качества
Земля	Север	Сила, стабильность, заземление
Огонь	Юг	Страсть, трансформация, энергия
Воздух	Восток	Интеллект, общение, вдохновение
Вода	Запад	Эмоции, интуиция, исцеление
Дух	Центр	Единство, превосходство, связь с божественным

В целом, пятиугольник имеет множество различных значений и интерпретаций в викканских и языческих традициях, но часто рассматривается как символ баланса, защиты и связи с миром природы. Независимо от того, носят ли его как украшение, используют ли в ритуалах или просто ценят за его красоту и значение, пятиугольник продолжает оставаться мощным и значимым символом в современной духовной практике.

Методы определения количества вершин у пятиугольника

Пятиугольник — это многоугольник, обладающий пятью вершинами. При определении количества вершин у пятиугольника можно использовать различные методы:

1. Геометрический метод: для определения количества вершин можно воспользоваться геометрическим подходом. Пятиугольник имеет пять сторон, следовательно, он должен иметь пять вершин.
2. Математический метод: можно воспользоваться математической формулой, которая позволяет определить число вершин многоугольника по его количеству сторон. Для пятиугольника формула будет следующей: число вершин = число сторон + 2, то есть 5 + 2 = 7.
3. Счетный метод: при данном методе можно просто посчитать количество вершин пятиугольника, обозначая каждую вершину числом. В результате получим, что пятиугольник имеет 5 вершин.

Описанные методы позволяют определить количество вершин у пятиугольника и применимы для различных типов многоугольников.

Математическая формула определения количества вершин

Количество вершин пятиугольника можно определить с использованием основной формулы для простых многоугольников:

Количество вершин = 2n

где n — количество сторон пятиугольника.

Таким образом, для пятиугольника, количество вершин будет:

Количество вершин = 2 * 5 = 10

Пятиугольник имеет 10 вершин.

Графический метод определения количества вершин

Графический метод — это один из способов определения количества вершин у пятиугольника. Он основан на визуальном анализе геометрической фигуры и ее свойств.

Для определения количества вершин у пятиугольника можно использовать следующий графический метод:

1. Нарисуйте пятиугольник.
2. Пронумеруйте вершины пятиугольника числами от 1 до 5.
3. Посчитайте количество вершин, обозначенных числами.

Например, если нарисованный пятиугольник имеет пять вершин, обозначенных числами от 1 до 5, значит, у этого пятиугольника пять вершин.

Если количество вершин не совпадает с числами, обозначенными на рисунке, значит, что-то было сделано неправильно при построении пятиугольника.

Графический метод является простым и наглядным способом определения количества вершин у пятиугольника. Он может быть использован как для учебных целей, так и в повседневной жизни.

Как классифицируются углы по величине?

Углы — это геометрические объекты, которые характеризуются величиной отклонения двух лучей друг от друга. В зависимости от величины этого отклонения углы могут быть классифицированы на несколько типов.

Прямой угол: угол, который составляет 90 градусов и делит плоскость на две равные части, называется прямым углом.

Острый угол: угол, который составляет менее 90 градусов и является более заточенным, называется острым углом.

Тупой угол: угол, который составляет более 90 градусов и является менее заточенным, называется тупым углом.

Таким образом, классификация углов по величине помогает легче ориентироваться в геометрическом пространстве и определять взаимное расположение геометрических объектов.

Конструкция правильного пятиугольника

Правильный пятиугольник — это многоугольник, у которого все стороны и все углы равны друг другу. Для построения правильного пятиугольника существуют различные методы:

1. Метод рисования окружностей
2. Метод конструкции по стороне
3. Метод конструкции по диагонали

Первый метод основан на рисовании нескольких окружностей, которые пересекаются в определенных точках. Для построения правильного пятиугольника с помощью этого метода нужно:

1. Нарисовать окружность с центром в точке O
2. Провести пять радиусов, начиная с точки O и с радиусом, равным длине стороны пятиугольника
3. Точки пересечения этих радиусов с окружностью образуют вершины пятиугольника
4. Соединить вершины пятиугольника линиями

Второй метод основан на построении правильного пятиугольника по заданной стороне. Для этого нужно:

1. На отрезке AB построить правильный треугольник ABC
2. Провести окружность с центром в точке C и радиусом, равным стороне пятиугольника
3. Точки пересечения этой окружности с отрезками BC и AC образуют вершины пятиугольника
4. Соединить вершины пятиугольника линиями

Третий метод основан на построении правильного пятиугольника по заданной диагонали. Для этого нужно:

1. Построить прямоугольный треугольник ABC, у которого AC — заданная диагональ пятиугольника, а угол BAC — 36°
2. Провести окружность с центром в точке A и радиусом, равным диагонали пятиугольника
3. Точка пересечения этой окружности со стороной AB образует вершину пятиугольника
4. Соединить вершину пятиугольника с вершинами треугольника B и C линиями

Таким образом, существует несколько способов конструкции правильного пятиугольника, использующих окружности и заданные стороны или диагонали. Эти методы позволяют построить пятиугольник с точностью до измерения углов и сторон.

Примеры применения на практике

Ниже приведены несколько примеров, которые иллюстрируют применение методов для нахождения центра пятиугольника.

1. Пример 1:

   Представим, что у нас есть пятиугольник ABCDE, заданный координатами вершин:

   • А(2, 5)
   • B(6, 7)
   • C(8, 4)
   • D(5, 2)
   • E(3, 3)

   Для нахождения центра пятиугольника можно воспользоваться формулой:

   x = (x1 + x2 + x3 + x4 + x5) / 5

   y = (y1 + y2 + y3 + y4 + y5) / 5

   Применим эту формулу к данному примеру:

   • x = (2 + 6 + 8 + 5 + 3) / 5 = 4.8
   • y = (5 + 7 + 4 + 2 + 3) / 5 = 4.2

   Таким образом, центр пятиугольника ABCDE имеет координаты (4.8, 4.2).

2. Пример 2:

   Предположим, у нас есть пятиугольник XYZWV с известными длинами его сторон:

   • XY = 5 cm
   • YZ = 3 cm
   • ZW = 7 cm
   • WV = 6 cm
   • VX = 4 cm

   Для нахождения центра пятиугольника, можно воспользоваться формулой:

   x = (x1 * l1 + x2 * l2 + x3 * l3 + x4 * l4 + x5 * l5) / (l1 + l2 + l3 + l4 + l5)

   y = (y1 * l1 + y2 * l2 + y3 * l3 + y4 * l4 + y5 * l5) / (l1 + l2 + l3 + l4 + l5)

   Где x1, x2, …, x5 и y1, y2, …, y5 — координаты вершин пятиугольника, l1, l2, …, l5 — длины его сторон. Применим эту формулу к данному примеру:

   • x = (x1 * l1 + x2 * l2 + x3 * l3 + x4 * l4 + x5 * l5) / (l1 + l2 + l3 + l4 + l5) = (x1 * 5 + x2 * 3 + x3 * 7 + x4 * 6 + x5 * 4) / (5 + 3 + 7 + 6 + 4)
   • y = (y1 * l1 + y2 * l2 + y3 * l3 + y4 * l4 + y5 * l5) / (l1 + l2 + l3 + l4 + l5) = (y1 * 5 + y2 * 3 + y3 * 7 + y4 * 6 + y5 * 4) / (5 + 3 + 7 + 6 + 4)

   Таким образом, центр пятиугольника XYZWV находится на точке с координатами (x, y).

3. Пример 3:

   Представим, что у нас есть пятиугольник PQRST, где известны координаты двух противоположных вершин:

   • P(1, 3)
   • R(7, 9)

   Для нахождения центра пятиугольника можно воспользоваться формулой:

   x = (x1 + x2) / 2

   y = (y1 + y2) / 2

   Применим эту формулу к данному примеру:

   • x = (1 + 7) / 2 = 4
   • y = (3 + 9) / 2 = 6

   Таким образом, центр пятиугольника PQRST имеет координаты (4, 6).

Смотреть что такое «Правильный пятиугольник» в других словарях:

Таким образом, создав фигуру с восемью сторонами разной длины, вы получите неправильный восьмиугольник. Существуют многоугольники с пересекающимися сторонами. Например, пятиконечная звезда является многоугольником с пересекающимися сторонами. Правильные многоугольники уже в глубокой древности считались символом красоты и совершенства. Практическая задача построения таких многоугольников с помощью циркуля и линейки имеет давнюю историю.

Лишь в 1796 г. К. Ф. Гаусc доказал принципиальную невозможность этого построения с помощью только циркуля и линейки. В настоящем параграфе мы предлагаем вам самим поискать способы построения правильных многоугольников, вписанных в данную окружность или имеющих заданную сторону

Не менее важное практическое значение имеют методы приближенного построения в тех случаях, когда точное построение циркулем и линейкой неосуществимо

Правильный пятиугольник — это многоугольник, у которого все пять сторон и все пять углов равны между собой. Вокруг него легко описать окружность. Теперь на окружности радиуса AО от любой точки последовательно отложим 11 дуг, каждая из которых равна дуге АВ. Получим вершины правильного двенадцатиугольника. Построение правильного пятиугольника по данной его стороне. Намечаем на окружности точку 1 и принимаем её за одну из вершин пятиугольника.

Эта фигура является многоугольником с минимальным количеством углов, которым невозможно замостить площадь. Только у пятиугольника количество диагоналей совпадает с количеством его сторон. Воспользовавшись формулами для произвольного правильного многоугольника, можно определить все необходимые параметры, которые имеет пентагон. Например, вписать его в окружность с заданным радиусом либо построить на базе заданной боковой стороны.

Как правильно начертить луч и какие принадлежности для черчения вам понадобятся? Возьмите листок бумаги и отметьте в произвольном месте точку. Затем приложите линейку и проведите линию, начиная с указанной точки и до бесконечности. Чтобы начертить ровную линию, нажмите клавишу «Shift»и проведите линию нужной длины. Сразу после начертания откроется вкладка «Формат». Уберите выделение с линии и увидите, что в начале линии появилась точка. Для создания надписи нажмите кнопку «Нарисовать надпись» и создайте поле, где будет находиться надпись.

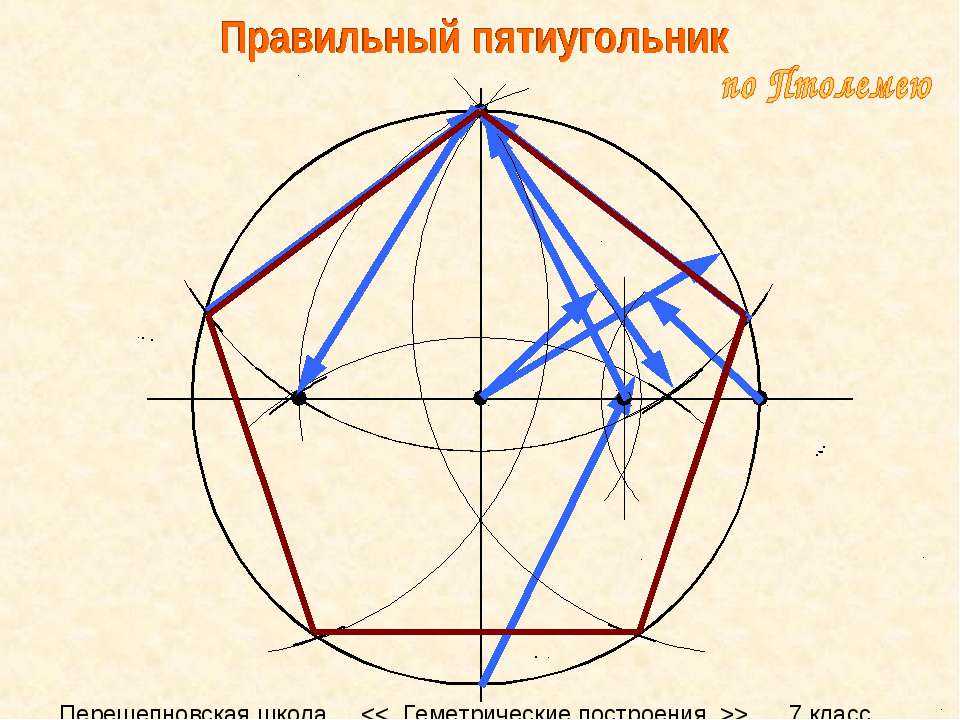
Первый способ построения пятиугольника считается более «классическим». Получившаяся в результате построения фигура будет правильным пятиугольником. Двенадцатиугольник не является исключением, поэтому его построение будет невозможным без применения циркуля. Задача построения правильного пятиугольника сводится к задаче деления окружности на пять равных частей. Начертить пентаграмму можно с использованием простейших инструментов.

Я долго бился пытаясь этого добиться и самостоятельно найти пропорции и зависимости, но мне этого не удалось. Оказалось, что есть несколько различных вариантов построения правильного пятиугольника, разработанных известными математиками. Инересным моментов является то, что арифметически эту задачу решить только приблизительно точно, поскольку придется использовать иррациональные числа. Зато ее можно решить геометрически.

Деление окружностей. Точки пересечения этих линий с окружностью и являются вершинами квадрата. В окружности радиуса R (Шаг 1) следует провести вертикальный диаметр. В точке сопряжения N прямой и окружности прямая является касательной к окружности.

Виды многоугольников

Различают несколько видов этих фигур: выпуклые, вогнутые, правильные и неправильные.

Какие многоугольники называются выпуклыми и невыпуклыми (вогнутыми)? Чтобы определить, какой многоугольник называется выпуклым, достаточно знать его определение.

Если стороны, при продолжении до прямой линии, не пересекают плоскость, то это выпуклый многоугольник.

Определение невыпуклого многоугольника: если при продолжении сторон прямые линии пересекают плоскость фигуры, то она является вогнутой.

Что такое правильные многоугольники

Выпуклые многоугольники, у которых все стороны и все углы равны, называются правильными.

На рисунке показан правильный многоугольник.