Скорость звука, критическая скорость и число маха. 1 мах это сколько

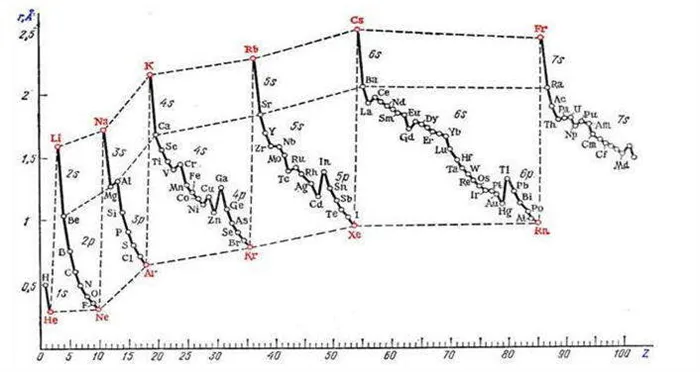
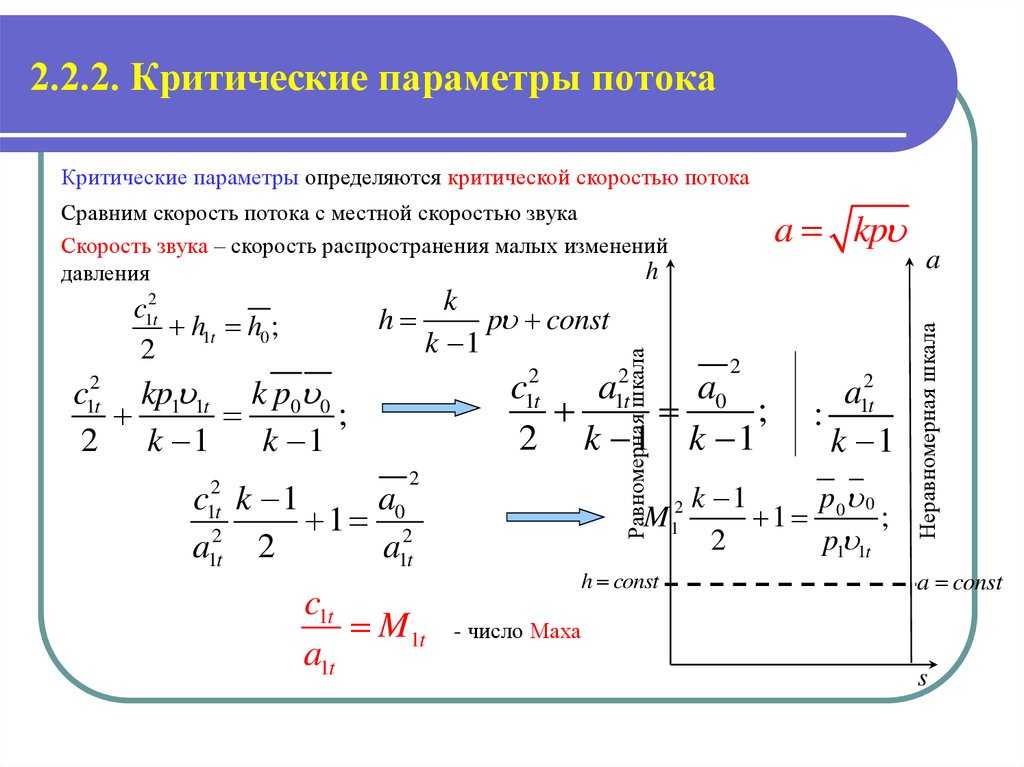
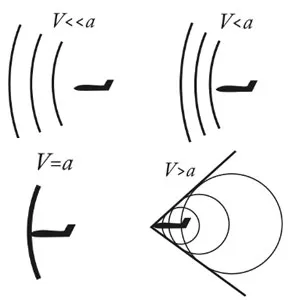
Типы обтекания летающего объекта

В общем, за исключением препятствий, это нарушение распространяется одинаково во всех направлениях. Таким образом, через секунду он оказывается распределенным по сфере радиусом 340 метров. Поскольку поверхность сферы пропорциональна квадрату ее радиуса, интенсивность возмущения очень быстро уменьшается с расстоянием: это основная причина затухания звука, гораздо более важная, чем вязкость.

В дальнейшем летающий объект, равномерно движущийся со скоростью V, будет уподобляться точке.

Дозвуковой поток

Если V < a (то есть Ma <1), летящий объект имеет скорость ниже, чем скорость увеличения сфер возмущения, которые он создает в каждый момент времени. Кроме того, он постоянно находится внутри созданных ранее. Любой может испытать это явление: неподвижный наблюдатель ощущает очень слабый звук первых очень расширенных сфер, затем интенсивность увеличивается, пока летящий объект не приближается, и, наконец, уменьшается до исчезновения.

Кроме того, смещение точки излучения сфер возмущения вызывает эффект Доплера .

Звуковой поток

Если Ma = 1, летающий объект постоянно прилипает к передней части всех сфер, созданных ранее, которые, следовательно, все касаются плоскости, перпендикулярной движению летающего объекта. Наложение множества мелких возмущений создает большое возмущение, которое значительно увеличивает сопротивление воздуха: это звуковой барьер .

Сверхзвуковой поток

Напротив, при Ma > 1 летающий объект оставляет за собой все сферы возмущения. Простые рассуждения показывают, что все они касаются конуса, называемого конусом Маха.

Махины в км в час: влияние скорости

Увеличение скорости махов в км в час:

Увеличение скорости махов позволяет достичь более высоких показателей производительности. Чем выше скорость махов, тем быстрее они смогут перемещаться в указанном направлении и выполнять свои функции.

Однако, повышение скорости махов требует соответствующих внешних условий и возможностей. Во-первых, необходимо обеспечить надлежащую систему торможения, чтобы снизить риск аварийных ситуаций и обеспечить безопасность работы. Во-вторых, повышение скорости может привести к увеличению износа и требованиям к техническому обслуживанию махов.

Снижение скорости махов в км в час:

Снижение скорости махов может быть необходимо в некоторых случаях, например, для выполнения сложных маневров или работы в ограниченном пространстве. Уменьшение скорости позволяет улучшить точность управления и предотвратить возникновение аварийных ситуаций.

Снижение скорости махов может быть достигнуто путем установки специальных устройств, таких как тормоза или регуляторы скорости.

Подведение итогов:

Скорость играет важную роль в работе махов, влияя на их производительность и возможности. Понимание влияния скорости и выбор оптимальных параметров махов позволяет повысить эффективность работы и обеспечить безопасность.

Comprehensive guide to speed unit conversion: machs to kilometers per hour and more

Understanding how to convert speed measurements like machs to kilometers per hour, and vice versa, is important to achieve exactness in your calculations.

How to convert machs to km/h

To convert from machs to kilometers per hour:

• Use the conversion factor: 1 mach equals 1225.04 kilometers per hour.
• For example, to convert 5.8 mach to km/h, calculate , which is .
• The formula is: speed in km/h = speed in mach x 1225.04

How to convert km/h to machs

For converting kilometers per hour to machs:

• Remember, 1 kilometer per hour is approximately 0.000816297 machs.
• To convert 7105.26 km/h to mach, multiply , resulting in .
• The conversion formula is:

Проблемы сверхзвукового полета

Каким бы ускоренным ни был нормальный самолет, он долго не сможет летать на сверхзвуковых скоростях. Дозвуковые плоскости более гладкие и округлые. А при полете на сверхзвуковых скоростях возникают другие аэродинамические условия.

Резко возрастает сопротивление воздуха, корпус самолета нагревается от трения. В результате обычный самолет потеряет устойчивость и может начать рушиться прямо в воздухе.

Сверхзвуковая авиация стала активно развиваться в 1950-1960-х годах. Первым серийным сверхзвуковым самолетом стал истребитель North American F-100 Super Sabre. Эта модель впервые полетела в 1953 году.

Также были созданы сверхзвуковые пассажирские самолеты, которые выполняли регулярные рейсы. Но их было всего 2: советский Ту-144 и англо-французский «Конкорд.

Сверхзвуковой пассажирский самолет Ту-144

Преимущество таких самолетов в том, что они могут преодолевать большие расстояния за короткий промежуток времени. Кроме того, сверхзвуковой самолет летит на большей высоте, чем обычный самолет. В результате воздушное пространство не перегружено. Но от их использования вскоре отказались из-за ряда недостатков:

• ударная волна;
• большой расход топлива;
• сложность операции;
• шум над аэродромом.

Громкий хлопок — это внезапное повышение давления перед летательным аппаратом, которое происходит, когда летательный аппарат начинает двигаться со сверхзвуковой скоростью (преодолевает звуковой барьер). Ударная волна перед летательным аппаратом распространяется по конусу. Человек, наблюдающий за полетом самолета, слышит аплодисменты, когда эта волна достигает его, и только тогда слышен двигатель. Ударная волна постоянно сопровождает самолет со сверхзвуковой скоростью. Однако хлопки в ладоши будут слышны только при пролете самолета в определенной точке, близкой к наблюдателю.

Скорость звука

Скорость звука A определяется как скорость распространения малого возмущения (тип 1)

где DP — увеличение давления DP — увеличение плотности.

Поскольку процесс распространения малых возмущений можно считать изоэнтропийным (т.е. без теплообмена и потерь)

где ρ — давление в среде, н/м2, ρ — плотность среды, кг/м3, R — газовая постоянная, нм/кг 0 К, T — температура, 0 К. k — изотропный экспонент, преобразующий теплоемкость газа при постоянном давлении в теплоемкость при постоянном объеме, определяется

Производные dp/(p x ρ) этих уравнений определяются с учетом следующего соотношения

Если пренебречь влиянием производной dz / dT, то скорость звука определяется уравнением 2.

Значение скорости звука зависит от притока (или оттока) тепла или механической работы, так как температура газа T может меняться. Однако уравнения 1 и 2 остаются в силе для воздействия на газы, которые не вызывают химических реакций.

Конечно, это можно легко объяснить тем, что изменения плотности и волнового давления можно рассматривать как малые, но конечные величины, в то время как толщина волны δ настолько мала, что ее следует считать минутной.

Таким образом, сила массы, переходящая через звуковую волну, обеспечивает условия, которые на порядки больше, чем изменения плотности или давления.

Критическая скорость

Во многих случаях полезно использовать понятие критической скорости αx, которая относится к локальной скорости, равной скорости звука, вместе со скоростью звука.

Для определения критической скорости используется общее уравнение сохранения энергии

Уравнение критической скорости

где T_* — критическая температура.

С другой стороны, скорость a_* например, скорость звука, определяется следующими уравнениями.

Из последних двух уравнений имеем

Где. — скорость звука в неподвижной среде.

Поэтому скорость звука в воздухе

Число Маха

Скорость потока пропорциональна скорости звука, а в некоторых случаях даже быстрее.

В таких случаях важной характеристикой потока является отношение скорости потока к скорости звука. Формула для определения числа Маха выглядит следующим образом

Формула для определения числа Маха выглядит следующим образом

где w — скорость потока в среде, а α — скорость звука.

Число Маха является одним из основных критериев подобия потока для определения явлений сжимаемости. Известно, что при ультразвуковых скоростях свойства потока резко меняются.

Важность числа Маха заключается в том, что оно показывает, превышает ли скорость потока газообразной среды скорость звука. Действительно, если M > 1, это означает, что поток движется быстрее скорости звука

Действительно, если M > 1, это означает, что поток движется быстрее скорости звука.

Тогда, если M1 — ультразвуковой. Кроме того, это не все потоки жидкости.

Есть еще несколько. Как вы уже знаете, скорости от 1 до 5 Махов называются ультразвуковыми; от 5 до 23 Махов — ультразвуковыми 23 Маха и выше — первая космическая скорость.

Числа Маха являются безразмерными величинами, но для понимания их порядка во многих источниках приводятся в единицах системы СИ. Это означает, что число Маха должно быть в километрах в час.

В этом случае один Мах соответствует 1 199 км/ч или 333 м/с

Обратите внимание, однако, что эти значения достигаются при нормальном атмосферном давлении и нулевой температуре и влажности на поверхности почвы

Поскольку давление, температура и влажность изменяются на разных высотах от земли, меняется и скорость звука.

Так, например, для истребителя, летящего со скоростью 2,3 Маха или 2 450 км/ч на высоте 18 000 м над землей, 1 Мах будет равен 1065 км/ч или 295 м/с.

Этимология

Число Маха названо в честь моравского физика и философа Эрнста Маха и является обозначением, предложенным авиационным инженером Якобом Акеретом в 1929 году. Поскольку число Маха является безразмерной величиной, а не единицей измерения, число следует за единицей; второе число Маха — 2 Маха вместо 2 Маха (или Маха). Это чем-то напоминает ранний современный знак единицы измерения глубины океана (синоним сажени ), который также был первым единицей измерения и, возможно, повлиял на использование термина Мах. В течение десятилетия, предшествовавшего , авиационные инженеры называли скорость звука числом Маха , а не 1 Маха .

Экономика России в 2017 году – эксперты

Сейчас куда ни плюнь, куда не переключи свой зомбоящик – везде сидят высокие боссы в костюмах (или они так хотят себя преподнести для своих слушателей – а сами сидят в дырявых носках), суть не в этом. Вот сидят эти эксперты и рассказывают нам про экономику России в 2017 году, то что она только встаёт с колен, что следующий год 2018 будет гораздо продуктивней и всем станет жить веселее. Но мало кто задумывается, что с приходом нового президента в США, очень многое в мировой экономике и в том числе экономике России в 2017 – 2018 года очень всё сильно измениться.

Взять только один пример – когда новоиспечённый президент ослабит санкции против России, цены опять вырастут. Как знаете такую замечательную поговорку: Курс доллара взлетел – цены поднялись, курс доллара упал – цены всё равно поднялись, так значит дело не в курсе доллара – а в людях, которые эти самые цены и ставят в мировой экономике и в Российской в том числе.

Экономика России прогноз экспертов последние новости

Деловитые и бородатые эксперты (хотя как показывает ТВ и практика – скорее они уже лысые), начали твердить в последнее время о прогнозе экономики России. Про то что появились замечательные подвижки в сельском хозяйстве, что в космосе у нас конкурентов нет, да что уж тут приводить примеры и говорили что и санкции нам не страшны. Вот только экономика России согласно экспертам, за последние новости стало сводиться на нет – вместе с их прогнозами, которые, как и у синоптиков с вероятностью в 0.0001% сойдётся с погодой.

В общем-то, особо доверять этим экспертам не стоит – так как все эти прогнозы, касающиеся последних новостей экономики в России, не сходятся ни как. Но, тем не менее, читайте эти последние новости экономики за эту и прошлую неделю на нашем сайте – ведь здесь любят пиариться именно боссы своих прогнозов.

Выбор редакции>> Все статьи

В Морозовской детской больнице открыли новый корпус

14-09-2017, 18:30

В столице завершилось строительство новой Морозовской детской больницы. На месте старых построек еще 30-х годов выросло семиэтажное здание, оборудованное самыми современными аппаратами. Технологии помогут в лечении редких и тяжелых заболеваний. Когда там начнут принимать маленьких пациентов?

Читать далее

Новости>> Все статьи

50 жертв: ИГ взяла на себя ответственность за масштабный теракт в Ираке

Террористическая группировка «Исламское государство» (запрещена в РФ) взяла на себя ответственность за двойной теракт в Ираке, жертвами которого стали 50 человек, а ранения получили более 80 человек.

Фонд однокурсника Медведева ответил на статью о «ривьере» для премьера

В фонде «Дар» ответили на расследование о строительстве под Калининградом усадьбы для премьера Дмитрия Медведева площадью 16 га. Участок был куплен, но на нем ничего не строится, заявили в фонде

Доступ к ресурсу заблокирован за нарушение авторских прав, но по ресурсу выносились и другие судебные решения, заявили РБК в Роскомнадзоре. На момент публикации одно из зеркал сайта оставалось доступным

Проблемы возникающие при достижении восьми махов

Одна из основных проблем – нагревание. Скорость восьми махов вызывает интенсивное нагревание крыльев, фюзеляжа и других частей самолета. Это может привести к деформации и повреждениям материалов, что повышает риск аварии. Для предотвращения нагревания до опасных пределов, специалисты разрабатывают специальные материалы с высокой термической стойкостью и проводят детальное тепловое моделирование конструкции самолета.

Другая проблема – аэродинамические силы. При скорости восьми махов сила аэродинамического давления на поверхность самолета значительно увеличивается, что оказывает дополнительные нагрузки на структуру. Это может привести к деформации, возникновению трещин и отрыву крыла. Для решения этой проблемы используются специальные аэродинамические обтекатели и усиленные конструкции крыльев, способные выдерживать высокие нагрузки.

Еще одна проблема – жесткость самолета. При достижении восьми махов возникают сильные динамические нагрузки, которые могут вызывать деформации и разрушения самолета. Поэтому требуется исключительная жесткость конструкции, чтобы справиться с этими нагрузками. Современные самолеты, предназначенные для скорости восьми махов, обычно имеют жесткие и легкие конструкции, выполненные из высокопрочных материалов.

Наконец, одной из наиболее серьезных проблем при достижении восьми махов является управление самолетом. При такой высокой скорости авионика должна быть способна обрабатывать и реагировать мгновенно на все данные, чтобы поддерживать стабильность полета и предотвращать аварии. Это требует разработки и применения особых автоматических систем управления, которые способны компенсировать любые возникшие отклонения и поддерживать стабильность полета.

Все эти проблемы требуют значительных усилий и исследований со стороны инженеров и ученых, чтобы обеспечить безопасность и эффективность полетов при скорости восьми махов.

Махины в км в час: влияние на спорт

Махины в км в час играют значительную роль в развитии спорта. Скорость, достигаемая спортсменами, имеет огромное значение, определяя результаты соревнований и установление новых рекордов.

Спортивные автомобили, особенно в мировых чемпионатах по автоспорту, развивают впечатляющие скорости, достигающие более 300 км в час. Это позволяет гонщикам преодолевать трассу быстро и эффективно, выявляя самого сильного и ловкого.

Велоспорт также претерпел значительные изменения благодаря увеличению скорости махин. Специальные велосипеды, созданные для шоссейных гонок, позволяют спортсменам развивать высокие скорости, преодолевая длинные дистанции в кратчайшие сроки. Спортсмены на велосипедах, развивающих скорость около 50-60 км в час, не только стали более эффективными, но и вносят свой вклад в развитие и совершенствование этой дисциплины.

Гонки на лыжах, скоростной роликовый спорт и другие виды спорта, где важна высокая скорость передвижения, также получили новые возможности благодаря махинам в км в час. Спортсмены стали еще быстрее, смелее и находчивее, придумывая новые стратегии и тактики для достижения победы.

В общем, скорость, достигаемая махинами в км в час, дает спортсменам возможность выйти на новый уровень и показать свои выдающиеся способности. Это вдохновляет молодежь и способствует развитию спортивной культуры, создавая новые возможности для достижения великих побед.

Kilometers per hour (km/h): A Unit of Measurement for Speed

Kilometers per hour (km/h) is a unit of measurement commonly used to express speed in countries that use the metric system. It represents the number of kilometers traveled in one hour.

The formal definition of kilometers per hour (km/h) is straightforward: it represents the distance traveled in kilometers divided by the time taken to travel that distance in hours.

For example, if a train travels a distance of 100 kilometers in one hour, its speed would be expressed as 100 kilometers per hour (km/h).

Conversions to Other Units of Measurement:

1. Miles per Hour (mi/h): To convert kilometers per hour to miles per hour, multiply the speed in kilometers per hour by a conversion factor of approximately 0.621371. For example, 100 kilometers per hour is approximately equal to 62.1371 miles per hour.
2. Knots (kts): Knots are commonly used in aviation and maritime contexts. To convert kilometers per hour to knots, multiply the speed in kilometers per hour by a conversion factor of approximately 0.539957. For example, 100 kilometers per hour is approximately equal to 53.9957 knots.
3. Meters per Second (m/s): To convert kilometers per hour to meters per second, multiply the speed in kilometers per hour by a conversion factor of approximately 0.277778. For example, 100 kilometers per hour is approximately equal to 27.7778 meters per second.
4. Feet per Second (ft/s): To convert kilometers per hour to feet per second, multiply the speed in kilometers per hour by a conversion factor of approximately 0.911344. For example, 100 kilometers per hour is approximately equal to 91.1344 feet per second.
5. Mach: The Mach number represents the speed of an object relative to the speed of sound in the surrounding medium. Mach 1 is equal to the speed of sound. To convert kilometers per hour to Mach, divide the speed in kilometers per hour by the speed of sound in kilometers per hour. The speed of sound at sea level is approximately 1234.8 kilometers per hour. For example, if an aircraft is traveling at 1234.8 kilometers per hour, its speed is Mach 1.

Высокоскоростное обтекание объектов

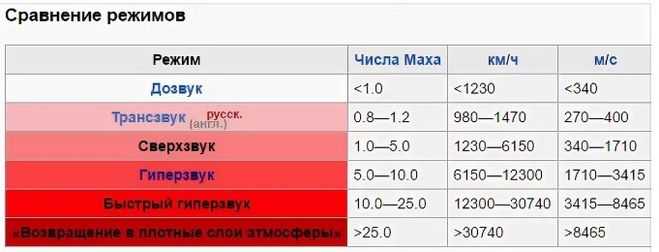
Полет можно условно разделить на шесть категорий:

Режим	дозвуковой	Трансзвуковой	Скорость звука	сверхзвуковой	гиперзвуковой	Гиперскорость
Маха	<0,8	0,8–1,2	1,0	1,2–5,0	5,0–10,0	>8,8

Для сравнения: требуемая скорость для низкой околоземной орбиты составляет примерно 7,5 км/с = 25,4 Маха в воздухе на больших высотах.

При трансзвуковых скоростях поле обтекания объекта включает как дозвуковую, так и сверхзвуковую части. Трансзвуковой период начинается, когда вокруг объекта появляются первые зоны течения с М > 1. В случае аэродинамического профиля (например, крыла самолета) это обычно происходит над крылом. Сверхзвуковой поток может замедлиться до дозвукового только в обычном скачке уплотнения; обычно это происходит перед задней кромкой. (Рис.1а)

С увеличением скорости зона течения M > 1 увеличивается как в сторону передней, так и в сторону задней кромки. При достижении и прохождении M = 1 нормальный скачок достигает задней кромки и становится слабым косым скачком: поток тормозится на скачке, но остается сверхзвуковым. Впереди объекта создается нормальный скачок, а единственная дозвуковая зона в поле течения — небольшая область вокруг передней кромки объекта. (Рис.1б)

(а)	(б)

Рис. 1. Число Маха при трансзвуковом обтекании профиля; М < 1 (а) и М > 1 (б).

Когда самолет превышает скорость 1 Маха (т. е. звуковой барьер ), непосредственно перед самолетом создается большая разница давлений . Эта резкая разность давлений, называемая ударной волной , распространяется назад и наружу от самолета в форме конуса (так называемый конус Маха ). Именно эта ударная волна вызывает звуковой удар , который слышен, когда над головой летит быстро движущийся самолет. Человек внутри самолета этого не услышит. Чем выше скорость, тем уже конус; при чуть более M = 1 это едва ли конус, но ближе к слегка вогнутой плоскости.

На полностью сверхзвуковой скорости ударная волна начинает принимать форму конуса, и поток становится либо полностью сверхзвуковым, либо (в случае тупого объекта) между носом объекта и ударной волной, которую он создает впереди, остается лишь очень небольшая область дозвукового течения. себя. (В случае острого предмета воздух между носом и ударной волной отсутствует: ударная волна начинается от носа.)

По мере увеличения числа Маха увеличивается сила ударной волны , и конус Маха становится все более узким. Когда поток жидкости пересекает ударную волну, его скорость уменьшается, а температура, давление и плотность увеличиваются. Чем сильнее шок, тем больше изменений. При достаточно больших числах Маха температура над ударной волной настолько возрастает, что начинается ионизация и диссоциация молекул газа за ударной волной. Такие течения называются гиперзвуковыми.

Ясно, что любой объект, движущийся с гиперзвуковой скоростью, также будет подвергаться воздействию тех же экстремальных температур, что и газ за носовой ударной волной, и, следовательно, выбор термостойких материалов становится важным.

8 махов в км в час: применение в авиации

8 махов в км в час представляют собой восьмеричную величину этой характеристики и означают, что самолет способен развивать скорость, в восемь раз превышающую скорость звука.

Применение скорости в 8 махов в км в час в авиации имеет несколько ключевых аспектов:

1. Повышенная эффективность полетов. Самолеты, способные летать со скоростью в 8 махов, могут демонстрировать более высокую эффективность полетов, что позволяет существенно сократить время воздушных перемещений. Это дает возможность осуществлять наиболее быстрые и комфортные перелеты.
2. Военное применение. Боевые самолеты, обладающие возможностью развивать скорость в 8 махов, получают преимущество в воздушных боях за счет возможности быстрого перемещения. Это позволяет им выполнять маневры, уворачиваться от противника и эффективно атаковать цели с большой скоростью.
3. Транспортировка грузов. Самолеты с высокой скоростью в 8 махов в км в час могут быть использованы для быстрой доставки грузов. Ускорение перевозки имеет особое значение при транспортировке грузов, требующих быстрой доставки из-за своего хрупкого или перегородочного характера.

В целом, скорость в 8 махов в км в час представляет собой важный параметр в авиации, который оказывает влияние на различные аспекты полета. Более высокая скорость не только позволяет сократить время перемещения, но и открывает новые возможности в области боевых действий и транспортировки грузов.

Восемь махов: что это и откуда они взялись

Вы наверняка слышали о понятии «восемь махов», но что они означают и откуда взялись?

Восемь махов — это фраза, которая обозначает скорость движения. На самом деле, мах — это древняя единица измерения времени, которая равна одному часу. Таким образом, восемь махов означает восемь часов. Но почему именно «мах»?

История этого понятия уходит корнями в Древней Греции. Во времена древних греков, существовало понятие «мах» — это был период времени, который требовался для движения Солнца от полудня до вечера. Граждане использовали это понятие для измерения времени, основываясь на движении Солнца.

С течением времени, «мах» был принят и в других странах, где он связывался с разными единицами времени. Например, в Древнем Риме «мах» был равен восьми часам, поэтому появилось понятие «восемь махов».

Сегодня «восемь махов» — это выражение, которое используют для обозначения быстрого движения или действия. Оно стало метафорой для выражения большой скорости или активности в каком-либо деле.

Теперь, когда вы знаете, что означает «восемь махов» и откуда они взялись, вы можете использовать это выражение в повседневной жизни или в разговоре с друзьями.

Обзор

Скорость звука (синий цвет) зависит только от изменения температуры на высоте (красный цвет) и может быть рассчитана исходя из него, поскольку изолированное влияние плотности и давления на скорость звука компенсирует друг друга. Скорость звука увеличивается с высотой в двух областях стратосферы и термосферы из-за тепловых эффектов в этих областях.

Число Маха является мерой характеристик сжимаемости потока жидкости : жидкость (воздух) ведет себя под влиянием сжимаемости аналогичным образом при заданном числе Маха, независимо от других переменных. Как смоделировано в Международной стандартной атмосфере , сухой воздух на среднем уровне моря , стандартная температура 15 ° C (59 ° F), скорость звука составляет 340,3 метра в секунду (1116,5 фута / с; 761,23 миль в час; 661,49 узлов). Скорость звука непостоянна; в газе она увеличивается пропорционально квадратному корню из абсолютной температуры , а поскольку атмосферная температура обычно снижается с увеличением высоты от уровня моря до 11 000 метров (36 089 футов), скорость звука также уменьшается. Например, в стандартной модели атмосферы температура снижается до -56,5 ° C (-69,7 ° F) на высоте 11 000 метров (36 089 футов) с соответствующей скоростью звука ( 1 Маха) 295,0 метров в секунду (967,8 футов / с; 659,9 миль в час; 573,4 узла), 86,7% от значения уровня моря.

Внешний вид в уравнении неразрывности

В качестве меры сжимаемости потока число Маха может быть получено из соответствующего масштабирования . Полное уравнение неразрывности для общего потока жидкости:

∂р∂т+∇⋅(рты)знак равно≡−1рДрДтзнак равно∇⋅ты{\ displaystyle {\ partial \ rho \ over {\ partial t}} + \ nabla \ cdot (\ rho {\ bf {u}}) = 0 \ эквив — {1 \ over {\ rho}} {D \ rho \over {Dt}}=\nabla \cdot {\bf {u}}}
производная по материалу , – плотность , – скорость потока . Для изоэнтропических изменений плотности, вызванных давлением, где скорость звука. Тогда уравнение неразрывности можно немного изменить, чтобы учесть это соотношение:ДДт{\ Displaystyle Д / Дт}р{\ Displaystyle \ ро}ты{\ displaystyle {\ bf {и}}}гпзнак равнос2гр{\ Displaystyle дп = с ^ {2} д \ ро}с{\ Displaystyle с}
−1рс2ДпДтзнак равно∇⋅ты{\ displaystyle — {1 \ over {\ rho c ^ {2}}} {Dp \ over {Dt}} = \ nabla \ cdot {\ bf {u}}}
Следующим шагом является обезразмеривание переменных как таковых:
Икс*знак равноИксл,т*знак равноUтл,ты*знак равнотыU,п*знак равно(п−п∞)рU2,р*знак равнорр{\ displaystyle {\ bf {x}} ^ {*} = {\ bf {x}} / L, \ quad t ^ {*} = Ut / L, \ quad {\ bf {u}} ^ {*} = {\ bf {u}} / U, \ quad p ^ {*} = (pp _ {\ infty}) / \ rho _ {0} U ^ {2}, \ quad \ rho ^ {*} = \ро /\ро _{0}}
где – характерный масштаб длины, – характерный масштаб скорости, – эталонное давление, – эталонная плотность. Тогда безразмерная форма уравнения неразрывности может быть записана как:л{\ Displaystyle L}U{\ Displaystyle U}п∞{\ Displaystyle р _ {\ infty}}р{\ Displaystyle \ ро _ {0}}
−U2с21р*Дп*Дт*знак равно∇*⋅ты*⟹−М21р*Дп*Дт*знак равно∇*⋅ты*{\ displaystyle — {U ^ {2} \ over {c ^ {2}}} {1 \ over {\ rho ^ {*}}} {Dp ^ {*} \ over {Dt ^ {*}}} = \nabla ^{*}\cdot {\bf {u}}^{*}\ подразумевает -{\text{M}}^{2}{1 \over {\rho ^{*}}}{Dp^{ *} \over {Dt^{*}}}=\nabla ^{*}\cdot {\bf {u}}^{*}}
где число Маха . В пределе уравнение неразрывности сводится к — это стандартное требование для течения несжимаемой жидкости