Порядок указания размеров
Если учитывать контекст, а также наиболее важную величину для конкретного объекта или изделия, тогда удастся правильно обозначить их габариты. Соблюдение данного правила позволяет определить, как идут размеры по порядку – длина, ширина, высота. Однако в определенных случаях устанавливаются индивидуальные стандарты последовательности обозначения габаритов.
Длина, ширина и высота представляют собой величины, которые позволяют измерить объект или изделие в трехмерном пространстве. В то же время длина является линейным продольным размером, тогда как ширина – это габарит в поперечном направлении.
Другим правилом, которого нужно придерживаться при указании габаритов, является обозначение сначала наибольшего размера. К примеру, когда описывается брусок 2800 × 40 × 22 мм, первое число означает длину, второе – ширину, а третья величина – это высота.

Итак, чтобы правильно указать последовательность размеров, нужно:
- определиться с рабочей поверхностью, являющейся лицевой частью объекта или изделия;
- понять, где у лицевой поверхности длина, ширина и высота;
- использовать длину при обозначении исключительно материальных объектов;
- придерживаться стандартного порядка записи габаритов, что подразумевает указание сначала длины, потом ширины, а затем высоты.
На заметку!
Кроме длины, ширины и высоты, при обозначении конструкции, материала или изделия еще могут применяться такие понятия, как глубина и толщина. Если какой-нибудь размер не используется (ДШВГТ), то он исключается из последовательности без нарушения порядка.
Из этого видео узнаете, как правильно писать размеры – ширина, высота, длина:
Использование буквы A
В математике площадь обычно обозначается буквой A. Это символ часто используется для обозначения площади геометрических фигур, таких как прямоугольники, треугольники, круги и т.д.
Например, площадь прямоугольника часто обозначается как A = ширина × высота, где A — площадь, ширина — длина одной из сторон прямоугольника, а высота — длина другой стороны.
Также, буква A может использоваться для обозначения площади в других областях математики, таких как теория вероятности и статистика.
Использование буквы A для обозначения площади является стандартной практикой и удобно для понимания и записи математических формул.
Маркировка дверных изделий
Поскольку изготовлением дверей занимается очень большое число компаний, то с маркировкой часто происходит путаница. Бывают ситуации, когда совершенно одинаковые конструкции, сделанные по одной технологии, не только по-разному называются (это еще вполне приемлемо), но и имеют разную маркировку. Все же для большинства моделей применяются общие нормы.
Для него существует следующая маркировка:
- Название ГОСТа;
- Высота в дециметрах;
- Дверь по ширине вместе с луткой в дециметрах;
- Буква «П» говорит, что это полотнище, а знак «Д» указывает, что оно сборное;
- «О» означает, что полотно застекленное, а знак «К», что дверь качающая.
Дополнительно есть символы, которые могут указывать, что изделие левостороннее (Л), у него есть порожек (П) и оно с наплавом (Н). Также каждая фабрика может ставить свои уникальные коды, предоставляя их расшифровку.
Классификацию ведут по нескольким направлениям и здесь в первую очередь учитывается, где будет располагаться дверь: внутри или снаружи (межкомнатная или внешняя)
Далее принимают во внимание материал изделия. Двери бывают деревянными, стальными, стеклянными и комбинированными
Указывается, что полотно глухое или остекленное. А в завершении учитывается число створок и какие они. Выделяют однопольную и двупольную конструкции. Также есть полуторные. Каждой модели присуждается официальное название.
Прямоугольник и его свойства
А теперь давайте вспомним о свойствах прямоугольника:
У прямоугольника все его диагонали равны;
Прямоугольник – это параллелограмм с параллельными противоположными сторонами;
Стороны прямоугольника в тоже время будут и его высотами;
Прямоугольник имеет равные противоположные стороны и углы;
Вокруг всякого прямоугольника можно описать окружность, притом диагональ прямоугольника будет равна диаметру описанной окружности.
Диагонали прямоугольника разделяют его на 2 равных треугольника;
Следуя теореме Пифагора, квадрат диагонали прямоугольника равен сумме квадратов 2-х его не противоположных сторон;

Задание:
1. Прямоугольник обладает такими двумя возможностями, при которых его можно поделить на 2 равных прямоугольника. Начертите в тетради два прямоугольника и разделите их так, чтобы получились 2 равных между собой прямоугольника.
2. Опишите вокруг прямоугольника окружность, диаметр которой будет равен диагонали прямоугольника.
3. Можно ли вписать в прямоугольник окружность так, чтобы она касалась всех его сторон, но при условии, что этот прямоугольник не является квадратом?
Вспомогательные знаки
Зачастую для упрощения нанесения размеров используются вспомогательные знаки. Например, деталь может иметь резьбовые или сквозные отверстия, зенковку, технологические уклоны, фаски, скругления и прочие элементы.
Обозначение фаски на чертежах можно выполнить различными способами в зависимости от масштаба, а также углов скоса и их количества. Важнейший критерий — это удобство чтения. При изготовлении не должно возникать излишних вопросов и сомнений. На чертеже обязательно ставятся два значения: величина угла относительно оси детали и ширина скоса. Наиболее часто встречающиеся фаски располагаются под углом 45°. Зачастую фаски обозначаются двумя линейными размерами, каждый из них имеет отметку о величине среза в различных плоскостях.
В некоторых случаях элементы с равными размерами указаны цифрами (1, 2…9 и т. д. ) в технических требованиях к чертежу, тогда на поле самого чертежа можно проставлять только номер этой ссылки. Такая простановка избавляет от проставления размера каждый раз.
Длина и ширина в математических формулах
В математике, понятие длины и ширины применяется для описания размеров и форм объектов или геометрических фигур.
Длина обычно определяется как расстояние между двумя точками на прямой или на кривой линии. В математической нотации длину часто обозначают символом «l» или «d». Например, для прямой линии AB, длина может быть обозначена как l_AB или d_AB.
Ширина, с другой стороны, чаще всего применяется для объектов двумерной природы, таких как прямоугольники или квадраты. Она определяется как расстояние между двумя противоположными сторонами фигуры. Ширина обычно обозначается символом «w» или «b». Например, для прямоугольника ABCD, ширина может быть обозначена как w_ABCD или b_ABCD.
Длина и ширина часто используются в формулах для вычисления площади и периметра различных геометрических фигур. Например, площадь прямоугольника может быть вычислена как произведение его длины на ширину — S = l * w.
Также, длина и ширина могут быть использованы для определения других характеристик геометрических фигур, таких как диагональ или радиус.
В математике, длина и ширина являются фундаментальными понятиями, используемыми для описания размеров объектов и проведения вычислений. Знание этих терминов позволяет более точно описывать и анализировать геометрические фигуры и решать различные математические задачи.
Понятие длины и ширины
Длина — это расстояние от одной точки объекта до другой вдоль его наиболее длинной стороны. Она измеряется с помощью линейки или маховика, и представляет собой одну из основных физических величин.
Например, длина может быть измерена для различных геометрических фигур, таких как отрезок, прямая, треугольник, параллелограмм, окружность и т.д. В каждом из этих случаев длина представляет собой расстояние между двумя точками, определенными по форме объекта.
Ширина — это расстояние от одного края объекта до другого, перпендикулярно его длине. Ширина может быть измерена для объектов различных форм и представляет собой расстояние, которое можно пройти в направлении, перпендикулярном длине. Например, ширина может быть измерена для прямоугольника или квадрата.
Длина и ширина играют важную роль в математике и науке. Они помогают нам классифицировать и описывать объекты, решать задачи, строить графики и диаграммы. Понимание этих понятий позволяет нам лучше понимать окружающий мир и применять математические методы для решения практических проблем.
Итак, длина и ширина — это основные измеряемые параметры объектов, которые помогают нам описывать и классифицировать различные фигуры и предметы.
Еще немного интересного
Итак, что такое прямоугольник, теперь понятно, но какую роль он играет в геометрических задачах и при измерениях на практике, еще предстоит разобраться. Так, в первую очередь надо сказать, что это наиболее удобная геометрическая фигура, при помощи которой можно делить площадь на участки и на открытой местности, и в помещениях.
Что такое прямоугольник? Как известно, он является четырехугольником. Существует множество разновидностей последнего, среди которых можно назвать трапецию (только две стороны равны), параллелограмм (противоположные стороны параллельны), квадрат (все углы и стороны одинаковые), ромб (параллелограмм с равными сторонами) и другие. Частным же случаем прямоугольника является квадрат, у которого все углы прямые, а стороны равны.
Нельзя говорить о том, что такое прямоугольник, и не упомянуть о том, как же определить его размеры. Площадью этой принято считать произведение ее ширины на длину, а периметр же, как и у любой фигуры, равняется сумме длин всех сторон. В данном случае он также равен удвоенной сумме длины и ширины, поскольку противолежащие стороны прямоугольника равны. Теперь вы знаете, что такое прямоугольник и что с ним делать, решая задачи и постигая секреты такой загадочной и таинственной науки, как геометрия.
Определение.
Прямоугольник
Прямоугольники отличаются между собой только отношением длинной стороны к короткой, но все четыре угла у них прямые, то есть по 90 градусов.
Длинную сторону прямоугольника называют длиной прямоугольника
, а короткую — шириной прямоугольника
.
Стороны прямоугольника одновременно является его высотами.
Виды прямоугольников по взаимному расположению сторон
Прямоугольник — это геометрическая фигура, у которой все углы прямые, а противоположные стороны равны. В зависимости от взаимного расположения сторон, прямоугольники могут быть разных видов:
- Квадрат – прямоугольник, у которого все стороны равны.
- Прямоугольник – прямоугольник, у которого две пары противоположных сторон равны.
-
Квадратный прямоугольник – прямоугольник, который одновременно является и квадратом, и прямоугольником.
Куб – трёхмерная фигура, у которой все ребра равны и все углы прямые.
- Криволинейный прямоугольник – прямоугольник, у которого хотя бы одна сторона является кривой линией.
Эти различные виды прямоугольников имеют свои особенности и применяются в различных областях математики, геометрии и инженерии.
Свойства и линии
Из-за того, что прямоугольник — это параллелограмм, все свойства последнего справедливы и к нему. В первую очередь для него характерно, что противоположные стороны являются параллельными, то есть лежат на непересекающихся прямых. Отсюда следует, что фигуры отличаются друг от друга только размерами двух граней.
К основным свойствам прямоугольника относят:
- противолежащие стороны имеют равную длину: AB = CD, BC = AD;
- все углы равны 90 градусов;
- отрезки, обозначающие ширину и длину, всегда перпендикулярные друг другу: AB ┴ BC, BC ┴ CD, CD ┴ AD, AD ┴ AB;
- сумма любых двух углов фигуры равняется 180 градусов, соответственно всех четырёх — 360;
- в четырёхугольном теле можно провести 2 диагонали, длины которых будут совпадать по величине: AB = BC;
- сумма квадратов диагональных отрезков равняется удвоенной сумме квадратов сторон фигуры: AC2 + BD2 = 2 (AB2 + BC2);
- построенная диагональ разделяет прямоугольник на 2 одинаковые фигуры — прямоугольные треугольники;
- точка пересечения прямых линий, соединяющая попарно противоположные углы, является центром фигуры и описанной окружности;
- диагонали в месте пересечения разделяются на 4 равных отрезка;
- в многоугольник, у которого длина не равна ширине, вписать окружность нельзя, поэтому её можно построить только для частных случаев прямоугольника.
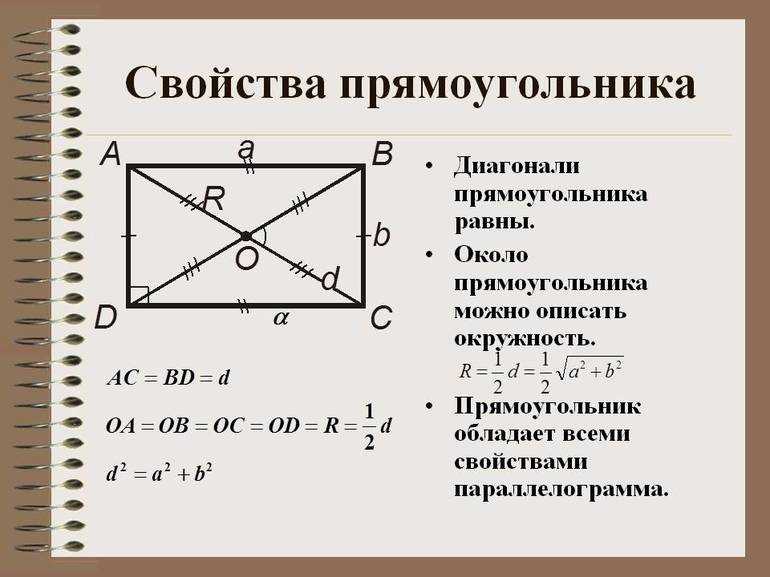
На свойстве, что сложенные квадраты диагоналей можно найти как сумму квадратов всех его сторон, построено решение многих геометрических задач. Нелишним будет доказательство теоремы. Пусть имеется прямоугольник, у которого линии AC и BD — диагонали. Если изобразить многоугольник на рисунке и построить отрезки, можно увидеть, что каждая диагональ делит фигуру на 2 треугольника: ABC и BDC.
Используя теорему косинусов, можно записать: AC2 = AB2 + BC2 — 2 * AB * BC * cos (ABC); BD2 = CD2 + BC2 — 2 * CD * BC * cos (BCD). После сложения полученных выражений получится запись: AC2 + BD2 = AB2 + BC2 — 2 * AB * BC * cos (ABC) + CD2 + BC2 — 2 * CD * BC * cos (BCD).
Так как по свойству прямоугольной фигуры противоположные стороны равны, уравнение примет вид: AC2 + BD2 = 2AB2 + 2BC2 — 2 * AB * BC * cos (ABC) — 2 * AB * BC * cos (BCD). Учитывая, что сумма двух углов равняется 180, полученное выражение можно переписать так: AC2 + BD 2 = 2 (AB 2 + BC 2). Что и следовало доказать.
Задача 4. Как найти ширину, зная диагональ
Эта задача уже немного сложнее предыдущих. В ней, кроме свойств прямоугольника, необходимо будет вспомнить формулы прямоугольных треугольников. Допустим, что диагональ АС прямоугольника АВСД равна 54,6 см, а соотношение длина-ширина — 16:9. Необходимо найти ширину фигуры.
Треугольник АВС имеет прямой угол, а значит, является прямоугольным. Диагональ — его гипотенуза, а стороны — катеты.
Из условия: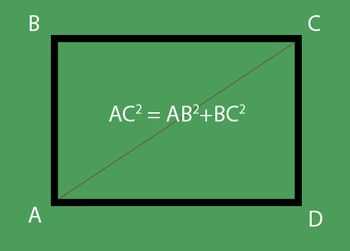
16АВ = 9ВС, отсюда АВ = 9ВС:16
По теореме Пифагора:
АС 2 = АВ 2 +ВС 2
Подставляем цифры:
- 54,62 = (9ВС:16) 2 +ВС 2
- 2981,16 = 81ВС 2:256+ВС 2
- 2981,16 = 337ВС 2:256
- 337ВС 2 = 763176,96
- ВС 2 = 2264,62
- ВС = 47,59 (см)
Ответ: ширина треугольника равна 47,59 см.
Основные свойства прямоугольника
Прямоугольником могут быть параллелограмм, квадрат или ромб.
1. Противоположные стороны прямоугольника имеют одинаковую длину, то есть они равны:
AB = CD, BC = AD
2. Противоположные стороны прямоугольника параллельны:
3. Прилегающие стороны прямоугольника всегда перпендикулярны:
AB ┴ BC, BC ┴ CD, CD ┴ AD, AD ┴ AB
4. Все четыре угла прямоугольника прямые:
∠ABC = ∠BCD = ∠CDA = ∠DAB = 90°
5. Сумма углов прямоугольника равна 360 градусов:
∠ABC + ∠BCD + ∠CDA + ∠DAB = 360°
6. Диагонали прямоугольника имеют одинаковой длины:
7. Сумма квадратов диагонали прямоугольника равны сумме квадратов сторон:
2d
2 = 2a
2 + 2b
2
8. Каждая диагональ прямоугольника делит прямоугольник на две одинаковые фигуры, а именно на прямоугольные треугольники.
9. Диагонали прямоугольника пересекаются и в точке пересечения делятся пополам:
| AO = BO = CO = DO = |
d |
||
| 2 |
10. Точка пересечения диагоналей называется центром прямоугольника и также является центром описанной окружности
11. Диагональ прямоугольника является диаметром описанной окружности
12. Вокруг прямоугольника всегда можно описать окружность, так как сумма противоположных углов равна 180 градусов:
∠ABC = ∠CDA = 180° ∠BCD = ∠DAB = 180°
13. В прямоугольник, у которого длина не равна ширине, нельзя вписать окружность, так как суммы противоположных сторон не равны между собой (вписать окружность можно только в частный случай прямоугольника — квадрат).
Ширина
Как было сказано выше, в математике рассматриваемая величина является одним из трех пространственных измерений любого объекта, при условии что его замеры производятся в поперечном направлении. Так чем знаменита ширина? Обозначение буквой «В» она имеет. Об этом известно во всём мире. Причем, согласно ГОСТу, допустимо применение как заглавной, так и строчной латинских литер. Часто возникает вопрос о том, почему именно такая буква выбрана. Ведь обычно сокращение производится по первой букве латинского, греческого или английского названия величины. При этом ширина на английском будет выглядеть как «width».
Вероятно, здесь дело в том, что данный параметр наиболее широкое применение изначально имел в геометрии. В этой науке, описывая фигуры, часто длину, ширину, высоту обозначают буквами «а», «b», «с». Согласно этой традиции, при выборе литера «В» (или «b») была заимствована системой СИ (хотя для других двух измерений стали применять отличные от геометрических символы).
Большинство полагает, что это было сделано, дабы не путать ширину (обозначение буквой «B»/«b») с весом. Дело в том, что последний иногда именуется как «W» (сокращение от английского названия weight), хотя допустимо использование и других литер («G» и «Р»). Согласно международным нормам системы СИ, измеряется ширина в метрах или кратных (дольных) их единицах. Стоит отметить, что в геометрии иногда также допустимо использовать «w» для обозначения ширины, однако в физике и остальных точных науках такое обозначение, как правило, не применяется.
Стандартные размеры кухонной мебели
Размеры кухонной мебели можно посмотреть на нижеприведенном рисунке.
Высоту рабочей поверхности разрабатывают высотой 850 мм. Глубину нижних кухонных шкафов логичнее выбрать в соответствии с размерами газовой или электрической плиты, если вы не планируете варочную панель. Стандартные размеры плит 500×500 или 600×600 мм. Глубину навесных шкафов и полок выбирайте размером 300 мм. Этот размер можно и уменьшить, но с учетом посуды и инвентаря.
Отделения для одежды и белья во встроенных шкафах будут оптимальными, если продумывать их под определенные вещи сразу. Но справочно, они приведены на следующем рисунке.
Размеры бельевых полок можно подсмотреть и на рисунке ниже, где в скобках указаны размеры для хранения постельного белья.
Расстояние же между самими полками должно быть в районе 200-400 мм. Если предполагается хранить головные уборы, полка под них должна быть глубиной не менее 240 мм, а высотой 170 мм.
Проектировать мебель необходимо и с учетом размеров и конфигурации самого помещения, учитывайте размеры проходов между изделиями, предусматривая различные группировки мебели.
В чем измеряются размеры длины, ширины и высоты по СИ
По единой системе измерения длина, высота и ширина измеряются в метрах. Но иногда, если это дробное или многозначное число, для удобства в вычислениях используют кратные единицы измерения.
Для того чтобы знать, как правильно переводить единицы измерения в более крупные или же наоборот мелкие, необходимо знать значения приставок.
После подсчетов эти единицы должны быть переведены в метры.
Существуют также внесистемные единицы, но они встречаются очень редко:
При выполнении геометрических заданий единицам измерения не уделяют особого внимания, главное, чтобы они были сопоставимы
(если вы производите подсчеты в сантиметрах, значит, все величины необходимо перевести в сантиметры).
А при решении физических задач ответ должен быть дан в метрах в соответствии с единой системой измерения.
Обозначения длины, ширины, высоты в геометрии
Измеряем геометрические параметры
Формулы прямоугольника:
Длина прямоугольника, b ширина прямоугольника, d диагональ и диаметр вокруг прямоугольника, r радиус вокруг прямоугольника, граница прямоугольника, s прямоугольник.
Виды сторон прямоугольника (длина и ширина прямоугольника): a
Тип диагностики прямоугольника:.
Тип периметра прямоугольника:.
Тип площади прямоугольника:.
Тип радиуса окружности, описанной вокруг прямоугольника:.
Примечание: Фото https://www.pexels.com и https://pixabay.com
Востребованные технологии
- Концепция инновационного развития общественного производства – осуществления Второй индустриализации России на период 2017-2022 гг. (106 949)
- Экономика Второй индустриализации России (103 205)
- Этилен (этен), получение, свойства, химические реакции (29 530)
- Программа искусственного интеллекта ЭЛИС (29 474)
- Метан, получение, свойства, химические реакции (26 578)
- Крахмал, свойства, получение и применение (26 050)
- Природный газ, свойства, химический состав, добыча и применение (25 168)
- Целлюлоза, свойства, получение и применение (24 320)
- Пропилен (пропен), получение, свойства, химические реакции (23 565)
- Прямоугольный треугольник, свойства, признаки и формулы (23 276)
О чём данный сайт?
Сайт посвящен научным разработкам автора в области экономики и научным идеям по осуществлению второй индустриализации России.
— Экономика второй индустриализации России, — Теория, методология и инструменты инновационного развития — Реализация второй индустриализации России — Организационные механизмы второй индустриализации России — Справочник по пионерным технологиям.
Мы не продаем продукты, технологии и т.д. Производители и изобретатели! Вам необходимо связаться с нами напрямую!
Мы ведем переговоры с производителями и изобретателями инновационных технологий в стране и даем рекомендации по их использованию.
О Второй индустриализации
Применение второй российской индустриализации основано на качественно новых научных данных (теория, методология и инструменты), разработанных авторами.
Конечным результатом второй индустриализации России является рост благосостояния всех членов общества. Это средний человек, бизнес и государство.
Вторая индустриализация России — это совокупность научных, технологических и других инновационных идей, планов и разработок, широко применимых к практике хозяйственной деятельности в краткосрочной перспективе (3-5 лет) и обеспечивающих новое прогрессивное развитие общества высокого качества. в ближайшие 50-75 лет.
Россия — первая страна, сделавшая это сложное открытие, — станет лидером мирового сообщества, чего не сможет сделать ни одна другая страна в течение столетий.
Определение понятия
Площадь указывает на размер плоскости, которую занимает фигура. Если вырезать любую фигуру из листа бумаги, положить на поверхность, а потом обвести карандашом, мы получим визуальное воплощение характеристики площади.
Площади двух абсолютно разных фигур могут быть одинаковыми. Почему так происходит? Потому что площадь – это характеристика. Можно провести простую аналогию с деньгами: сто грамм конфет и полкилограмма крупы стоят одинаково, но это совершенно разные вещи. Так треугольник и прямоугольник могут иметь одинаковую площадь. Фигуры, имеющие одинаковую площадь, называют равновеликими.
Что такое прямоугольник
В предыдущих классах вы уже изучали темы о прямоугольниках. Теперь давайте освежим память и припомним, что же это за такая фигура, которая носит название прямоугольник.
Прямоугольник — это параллелограмм, четыре угла которого являются прямыми и равняются 90 градусам.
Прямоугольник — это такая геометрическая фигура, состоящая из 4-х сторон и четырех прямых углов.
Противоположные стороны прямоугольника всегда равны.
Если рассматривать определение прямоугольника по евклидовой геометрии, то чтобы четырехугольник считался прямоугольником, необходимо, чтобы в этой геометрической фигуре, хотя бы три угла были прямыми. С этого следует, что и четвертый угол тоже будет девяносто градусам.
Хотя и так понятно, что когда сумма углов четырехугольника не имеет 360 градусов, то эта фигура не является прямоугольником.
В случае, когда у правильного прямоугольника все стороны равны между собой, то такой прямоугольник носит название квадрата.
В некоторых случаях квадрат может выступать в роли ромба, если у такого ромба кроме равных между собой сторон и все углы прямые.
Чтобы доказать причастность какой-либо геометрической фигуры к прямоугольнику, достаточно чтобы эта геометрическая фигура соответствовала как минимум одному из этих требований:
1. квадрат диагонали этой фигуры должен быть равен сумме квадратов 2-х сторон, которые имеют общую точку;
2. диагонали геометрической фигуры должны иметь одинаковую длину;
3. все углы геометрической фигуры должны равняться девяносто градусам.
Если эти условия отвечают хотя бы одному требованию, то перед вами прямоугольник.
Прямоугольник в геометрии является основной базовой фигурой, у которой имеется множество подвидов, со своими особыми свойствами и характеристиками.
Задание:
Назовите геометрические фигуры, которые относятся к прямоугольникам.
Где используется понятие ширины в математике

Ширина — это размерность фигуры в горизонтальной плоскости. Понятие ширины играет важную роль в геометрии и алгебре, так как позволяет оценивать размеры и расположение объектов относительно друг друга.
В геометрии, ширина используется при изучении геометрических фигур, таких как прямоугольники, квадраты и параллелограммы. Ширина примерно соответствует расстоянию между двумя параллельными сторонами фигуры.
Алгебра также использует понятие ширины при решении задач, связанных с графиками функций. Ширина графика функции определяется как длина отрезка оси x, на которой функция есть ненулевая.
В целом, понимание понятия ширины в математике является важным для решения многих задач в различных областях математики и естествознания.
Диагональ прямоугольника
Определение.
Диагональю прямоугольника
Формулы определения длины диагонали прямоугольника
1. Формула диагонали прямоугольника через две стороны прямоугольника (через теорему Пифагора):
d
= √a
2 + b
2
2. Формула диагонали прямоугольника через площадь и любую сторону:
4. Формула диагонали прямоугольника через радиус описанной окружности:
d
= 2R
5. Формула диагонали прямоугольника через диаметр описанной окружности:
d
= D о
6. Формула диагонали прямоугольника через синус угла, прилегающего к диагонали, и длину стороны противоположной этому углу:
8. Формула диагонали прямоугольника через синус острого угла между диагоналями и площадью прямоугольника
d
= √2S: sin β
ОСНОВНЫЕ ПОЛОЖЕНИЯ
1.1. Определенная величина обозначается буквой латинского или греческого алфавита без индексов или с индексами, служащими для уточнения различных характеристик этой величины.
1.2. Прописные и строчные буквы «О, о» латинского алфавита не должны употребляться в обозначениях. Буквы греческого алфавита следует принимать по табл. 1.
1.3. Буквенные обозначения необходимых величин, не приведенных в настоящем стандарте СЭВ, устанавливают по принципу, указанному в табл. 2.
Сила, произведение силы на длину, длина в степени, не равной единице
Прописные латинского алфавита
Длина, отношение длины ко времени в какой-либо степени, отношением усилия к единице длины или площади
Строчные латинского алфавита
Строчные греческого алфавита
1.4. Индексы подразделяются на цифровые и буквенные. Буквенные дополнительно подразделяются на одно-, двух- и трехбуквенные. Для обозначения цифровых индексов используются арабские цифры, а для обозначения буквенных индексов — буквы латинского алфавита.
1.5. Цифровые индексы применяются для выражения порядкового номера данного обозначения.
1.6. Однобуквенные индексы применяются для обозначения осей координат, расположения, вида материала, напряженного состояния, действующей нагрузки и других характеристик.
1.7. Двухбуквенные и трехбуквенные индексы применяются в том случае, когда использование однобуквенных индексов может привести к неясностям. Они отделяются от однобуквенных индексов запятыми.
1.8. Индексы располагаются с правой стороны букв внизу. При печатании на пишущей машинке букву и индекс допускается печатать на одной строчке.
1.9. Если в настоящем стандарте отсутствует необходимый индекс, его следует устанавливать из строчных букв латинского алфавита.
1.10. Обозначение, выражающее геометрическую величину, допускается дополнять вертикальным штрихом справа, если необходимо обозначить, что имеется ввиду сжатая часть сечения или элемента.


























